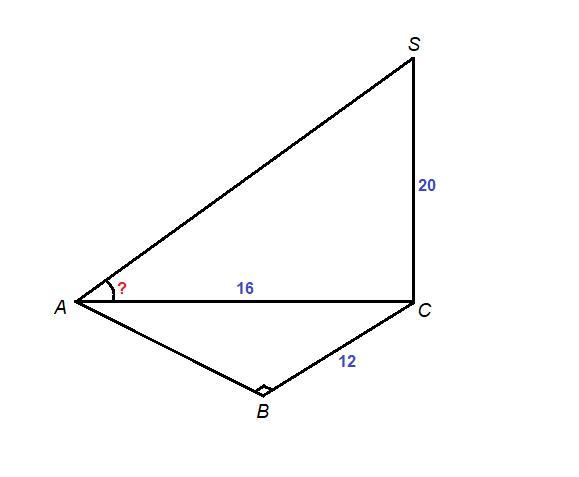
Дан прямоугольный треугольник ABC с гипотенузой AC=16 см и катетом BC=12 см.Отрезок SC=20 см,перпендикуляр к плоскости ABC.
а)Найдите SA;б)Найдите угол между прямой SA и плоскостью ABC.

Ответ:

а) SA = 4√41 см

б) ∠SAC = arctg 1,25

Объяснение:

а)

SC - перпендикуляр к плоскости треугольника АВС, значит и перпендикуляр к любой прямой этой плоскости.

ΔSAC:   ∠SCA = 90°, по теореме Пифагора:

SA = √(SC² + AC²) = √(20² + 16²) = √(400 + 256) = √656 = 4√41 см.

б)

• Угол между прямой и плоскостью равен углу между прямой и ее проекцией на эту плоскость.

AC - проекция SA на плоскость АВС, значит

∠SAC - угол между прямой SA и плоскостью (АВС).

Из прямоугольного треугольника SAC:

∠SAC = arctg 1,25