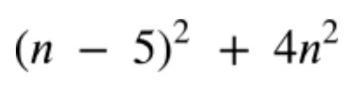Предмет: Алгебра
Автор: abnormal2213
Вопрос задан 2 года назад

< >

Докажите, что при всех целых значениях n выражение делится нацело на 5

Приложения:

Ответы

Ответ дал: 3metana

1

Ответ:

В решении

Объяснение:

$(n-5)^{2}+4n^{2}=n^{2}-10n+25+4n^{2}=5n^{2}-10n+25=5*(n^{2}-2n+5)$ . Один из множителей 5, значит, всё выражение делится на 5 при любом целом n.

Похожие вопросы

Русский язык

1 год назад

указать способ оброзование слов: беловатый, выпадает, пешеходные, причудливую, дорожки

Английский язык

1 год назад

ПОМОГИТЕ ПОЖАЛУЙСТА БАЛЛОВ НЕ ЖАЛКО

Қазақ тiлi

2 года назад

одағай сөзі бар халық əні

Английский язык

2 года назад

розповідь про улюбленого футболіста

Алгебра

7 лет назад

Розкладіть на множники квадратний тричлен: х2 + 6х + 5.

Литература

7 лет назад

ПОЖАЛУЙСТА!!!! СРОЧНО!!! ДАЮ ВСЕ БАЛЛЫ А. Платонова "Возвращение". 1.Что узнали о капитане Иванове 2.Кто или что является причиной изменений,произошедших в его семье? 3.Что такое война в

Математика

8 лет назад

Как найти площадь фигуры номер 1

Геометрия

8 лет назад

Найдите площадь ромба если его диагонаи равны 20 и 6