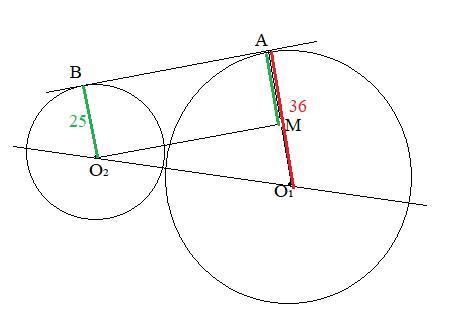
Окружность с центром О1 радиусом 36см и оуружность с центром О2 радиусом 25 см касаются внешним образом. АВ—общая касательная этих окружностей. Найдите площадь четырёхугольника АО1О2В. ​

"Окружность с центром О1 радиусом 36см и оуружность с центром О2 радиусом 25 см касаются внешним образом. АВ—общая касательная этих окружностей. Найдите площадь четырёхугольника АО1О2В"

Объяснение:

АО₁⊥АВ и О₂В⊥АВ по свойству радиуса , проведенного в точку касания.

Четырехугольник АО₁О₂В -трапеция, т.к О₁А║О₂В ,  по свойству , если две прямые перпендикулярны третьей , то они параллельны между собой.

S (трапеции) =1/2*h*(a+b) .

Пусть О₂М⊥АО₁ ,тогда МО₁=АО₁-АМ=36-25=11 (см),  О₂О₁ =25+36=61 (cм)

ΔО₂МО₁ -прямоугольный , по т. Пифагора

О₂Н=√(61²-11²)=√3600=60 (см)

S (трапеции) =1/2*60*(25+36)=1830 (см²) .