верно ли утверждение наибольшее расстояние между любыми двумя точками окружности равно длине её диаметра
Ответы
Ответ дал:
3
Докажем, что расстояние между любыми 2-мя точками окружности не больше диаметра.
Пусть A, B - 2 различные точки на окружности с центром O
Соединим A и B отрезком. Возможны два случая (см. рисунок):
1) O ∈ AB
В этом случае AB - диаметр, то есть AB равен диаметру.
2) O ∉ AB
В этом случае рассмотрим ΔABO.
AB < AO + OB (неравенство треугольника), но AO + OB равно диаметру окружности, а значит AB меньше диаметра.
В итоге получаем, что AB не больше диаметра для любых двух точек окружности.
Приложения:
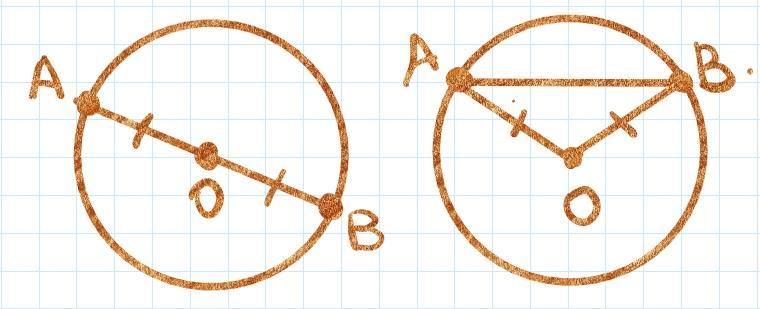
Похожие вопросы
1 год назад
1 год назад
2 года назад
7 лет назад
8 лет назад