Найдите объем конуса, если его образующая равна l, а осевым сечением является прямоугольный треугольник.

Ответ:

Пошаговое объяснение:

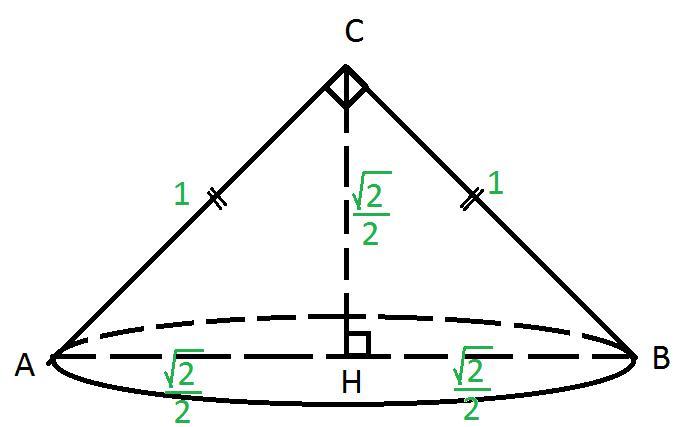
Рисунок к задаче на фото.

По условию задачи осевым сечением является прямоугольный треугольник, а образующая равна 1.

Значит осевым сечением является равнобедренный прямоугольный треугольник. Гипотенуза этого треугольника является диаметром основания. На рисунке это АВ.

По теореме Пифагора

Радиус основания

В равнобедренном прямоугольном треугольнике, высота, проведенная к гипотенузе равна половине гипотенузы.

Высота конуса

Вычислим объем конуса