Решите пж задачу
90 баллов дам

Приложения:

Ответы

Ответ дал: ldglkva

Ответ:

Объем пирамиды равен 324 кв. ед.

Объяснение:

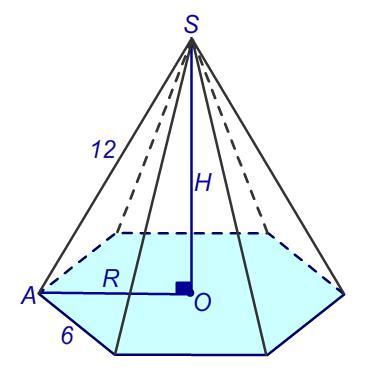
Сторона основания правильной шестиугольной пирамиды равна 6, боковое ребро равно 12. Найти объем пирамиды.

Дано:

правильная пирамида, основание - шестиугольник;

SA = 12 (боковое ребро);

a = 6 (сторона основания).

Найти: V.

Решение.

Объем пирамиды равен произведению одной третьей площади основания на ее высоту:
$\displaystyle V = \frac{1}{3}SH$
Пирамида называется правильной, если в ее основании лежит правильный многоугольник, а основание высоты пирамиды находится в центре основания пирамиды.
Высота пирамиды - это перпендикуляр, опущенный из вершины пирамиды на плоскость ее основания.

1) В основании нашей пирамиды лежит правильный шестиугольник.

Сторона правильного шестиугольника равна радиусу описанной около него окружности.

AO = R = 6.

2) Основание высоты SO пирамиды - точка O - является центром правильного шестиугольника: центром описанной окружности.

ΔAOS прямоугольный, ∠O = 90°, AO = 6. Найдем высоту пирамиды SO по т.Пифагора.

$\displaystyle SO^{2} = SA^{2} - AO^{2} = 12^{2} - 6^{2} = 144 - 36 = 108;\\\\SO = \sqrt{108} =\sqrt{36 \cdot 3} =6\sqrt{3}$

3) Найдем площадь основания пирамиды.

Площадь правильного шестиугольника определяется по формуле (a - сторона правильного шестиугольника):
$\displaystyle S_{6} = \frac{3a^{2}\sqrt{3} }{2}$