Катети прямокутного трикутника дорівнюють 5 см і 6 см. Знайдіть довжину медіанти трикутника, проведеної до більшого катета

Пусть АС = 5, АВ = 6.

Медиана СН - делит сторону АВ пополам ⇒ АН = 6 : 2 = 3.

Δ АСН - прямоугольный, ∠ А - прямой.

По теореме Пифагора ищем длину медианы СН:

СН = √АС² + АН = √5² + 3² = √25 + 9 = √34

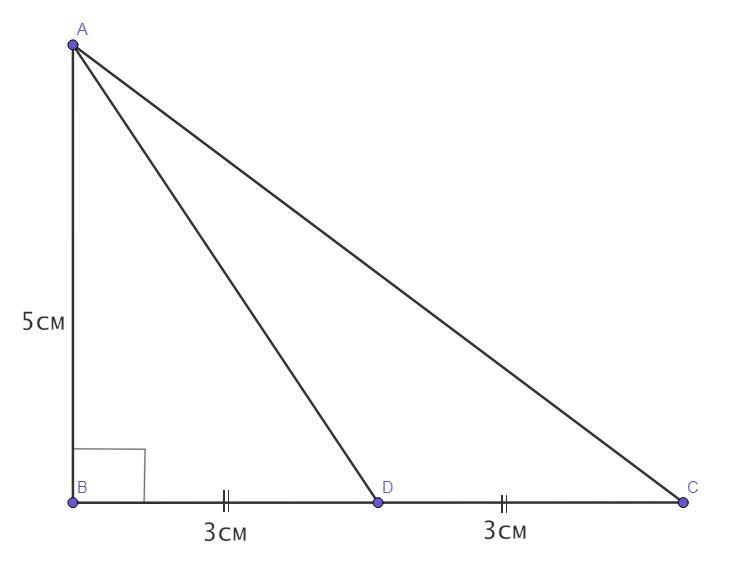
Чертёж смотрите во вложении.

Дано:

ΔАВС - прямоугольный (∠В = 90°).

АВ = 5 см.

ВС = 6 см.

AD - медиана.

Найти:

AD = ?

Решение:

BD = DC = 6 см/2 = 3 см. (так как AD - медиана и делит сторону пополам по определению).

Рассмотрим ΔBAD - прямоугольный (так как ∠В = 90° по условию).

Следовательно, по теореме Пифагора -

AD = √34 см.

Ответ: √34 см.