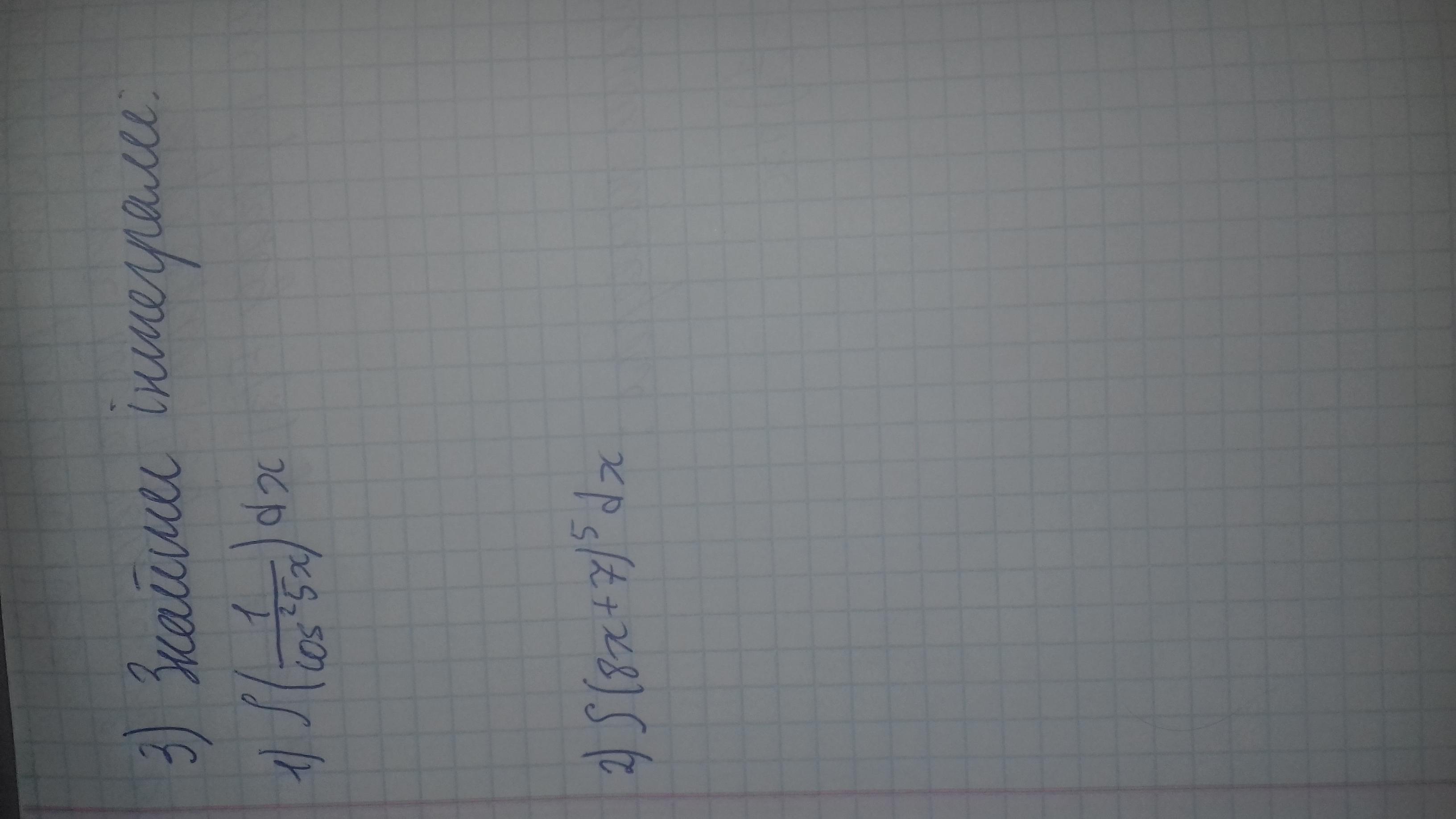Знайти інтеграл

Завдання на фото

Приложения:

Ответы

Ответ дал: bearcab

Ответ:

1) $\frac{1}{5}\tan(5x)+C$ , C=Const.

2) $\frac{(8x+7)^6}{48}+C,$ C=Const.

Объяснение:

$\int\frac{1}{\cos^2(5x)}\,dx=\int\frac{1}{5}*\frac{d(5x)}{\cos^2(5x)}=\frac{1}{5}\int\frac{d(5x)}{\cos^2(5x)}$

Если заменить 5x=t, то

$\frac{1}{5} \int\frac{d(5x)}{\cos^2(5x)}=\frac{1}{5}\tan(5x)+C,$ C=Const.

$\int (8x+7)^5\, dx=\int(8x+7)^5*\frac{1}{8}*d(8x)=\frac{1}{8}\int(8x+7)^5d(8x)=\frac{1}{8}\int(8x+7)^5d(8x+7)$

Если заменить (8x+7)=t, то

$\frac{1}{8}\int(8x+7)^5d(8x+7)=\frac{1}{8}*\frac{1}{6}*(8x+7)^6+C=\frac{(8x+7)^6}{48}+C$ , C=Const.

Похожие вопросы

Математика

1 год назад

Английский язык

1 год назад

Окружающий мир

2 года назад

Технология

2 года назад

Биология

7 лет назад

Математика

7 лет назад

История

8 лет назад

История

8 лет назад