ДАЮ 95 БАЛЛОВ. СЕГОДНЯ НАДО СДАТЬ
Найдите площадь криволинейной трапеции, ограниченной линиями:
1) у = х3 + 1, а = –1, b = 2
2) у = х2 – 2х + 1, а = –1, b = 1
3) у = 2 + 2х – х2, а = 0, b = 2
4) у = 3х2 – 4х, а = –2, b = –1
5) у = cos 2x, а = –π/4, b = π/4
Ответы
Ответ дал:
2
Ответ:
Пошаговое объяснение:
для всех примеров
площадь фигуры ограниченной функцией f(x), y=0, x=a. x=b численно равна значению определенного интеграла
вычисление интегралов на фото
Приложения:
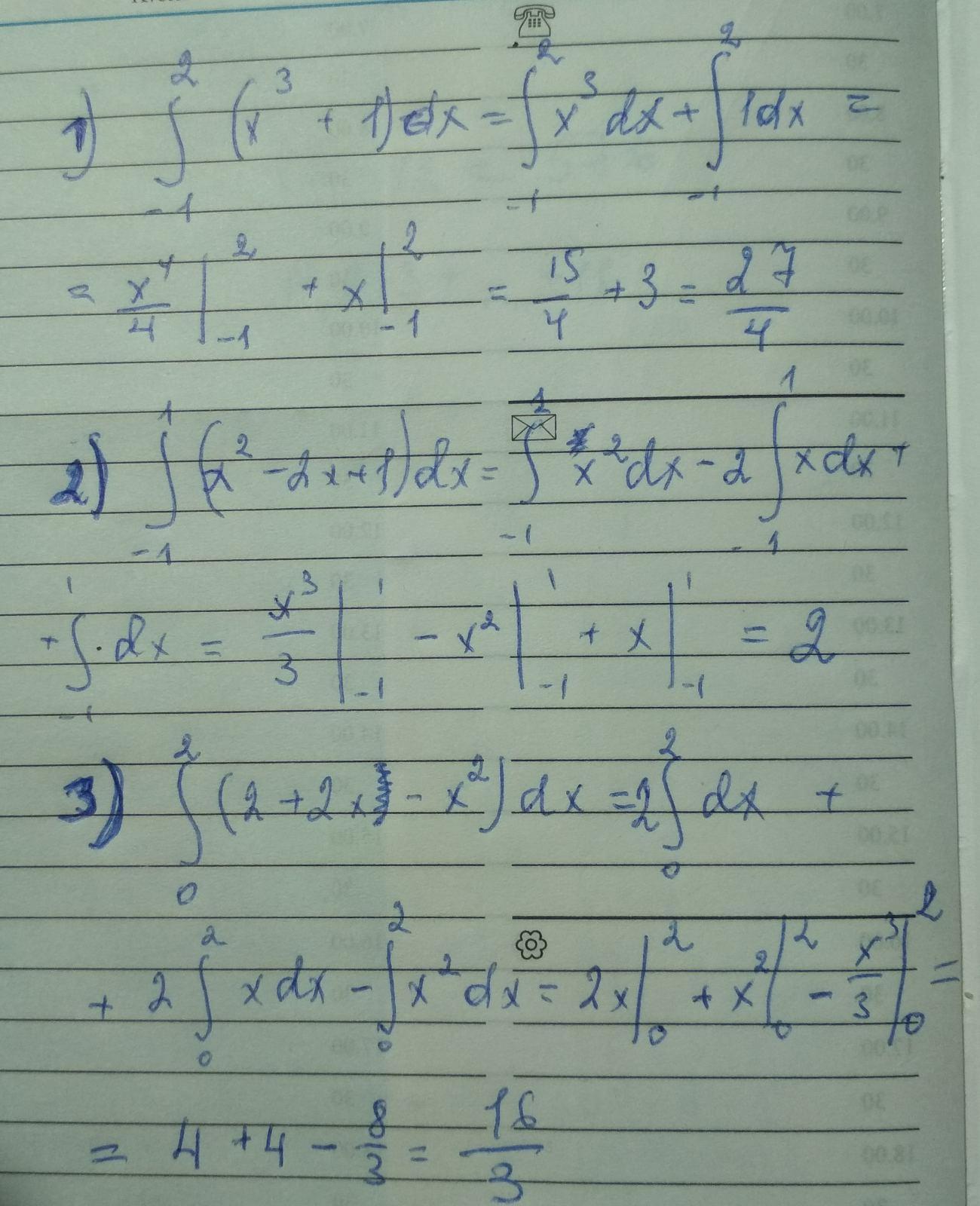

Похожие вопросы
1 год назад
1 год назад
2 года назад
2 года назад
7 лет назад
7 лет назад
8 лет назад