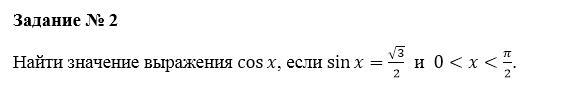Ответы
Ответ дал:
1
sinx=√3/2
sin²x+cos²x=1
cos²x=1-(√3/2)²
cos²x=1 - 3/4
cos²x=1/4
cosx=1/2 (1 четверть).
maziniury2014:
Спасибо большое, а можете сделать этот кружочек, какие в нём значения (с четвертями)
Уже нет. Чертим тригонометрический круг. Горизонтальная ось - косинус а; вертикальная - синус а. Разделим горизонтальный радиус пополам. (косинус а=1/2); из этой точки построим перпендикуляр к гориз. оси вверх до пересечения с окружностью в т.А. Из этой точки проведем перпендикуляр к вертикальной оси. Соединим т.А с центром круга. Точка А(х; у). х=cos a=1/2; y=sin a=V3/2. Все. V - знак корня. Это 1 четверть. Угол=60 гр.
Ответ дал:
0
В задании 2 :
в заданном диапазоне х косинус положителен. Из основного тригонометрического тождества квадрат косинуса равен 1-3/4=0,25
Значит косинус равен 0,5.
И правда : указанный диапазон - это углы прямоугольного треугольника и угол х равен 60 градусам. Синус равен корню из 3 пополам, а косинус 1/2.
В задании про 0 ничего не сказано, но замечу, что нулевого значения в этом интервале синус принимать не может (синус равен 0, если х равен пи*н, где н -любое целое)
Похожие вопросы
1 год назад
2 года назад
2 года назад
7 лет назад