знайдіть більшу діагональ прямокутної трапеції з основами 3 см і 6 см та кутом 120 градусів ​

Ответ:

√63 см.

Объяснение:

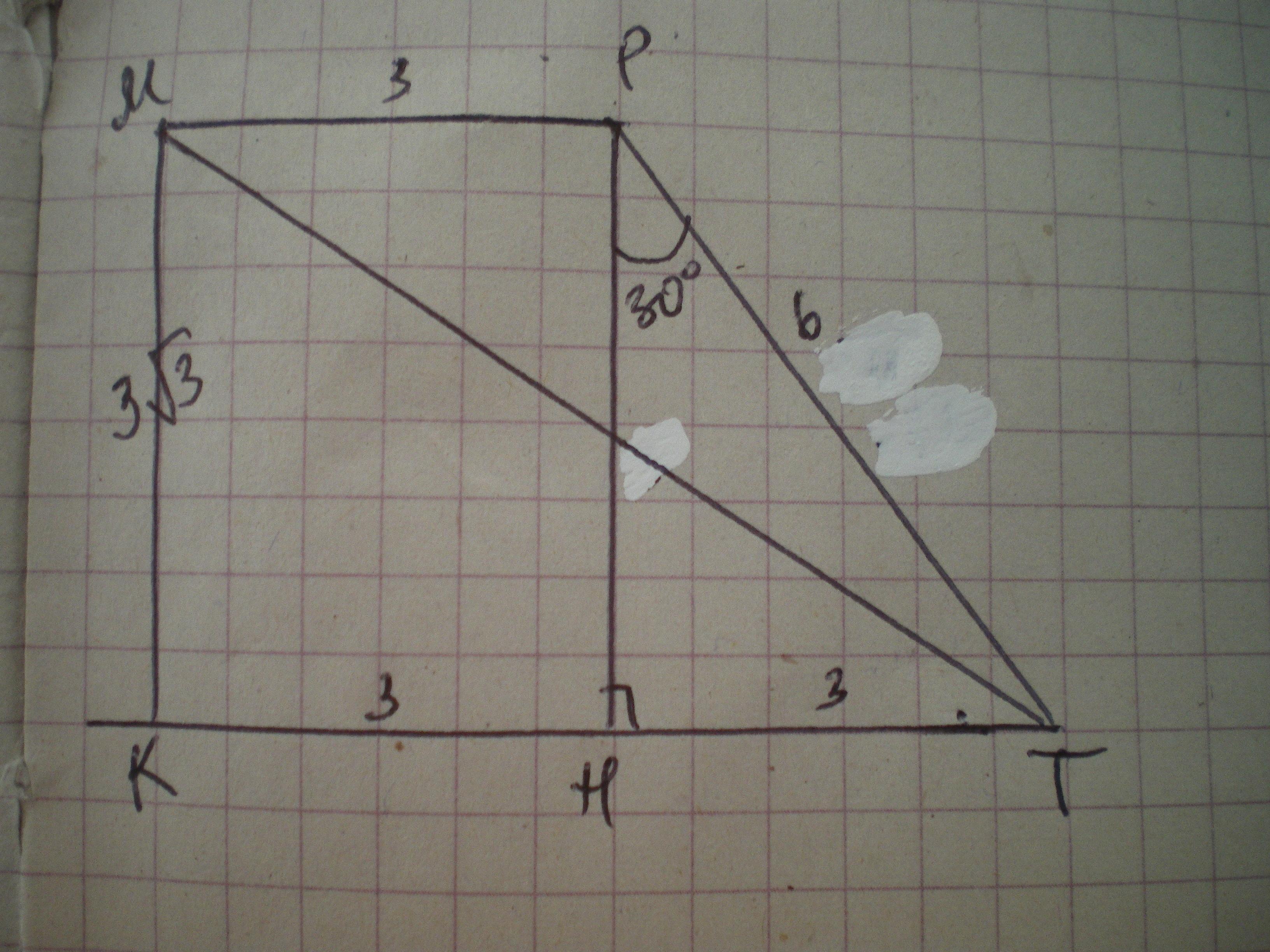
Дано: КМРТ - трапеція, МР=3 см, КТ=6 см, ∠МРТ=120°. Знайти МТ.

Проведемо висоту РН.  КН=МР=3 см, ТН=6-3=3 см.

Розглянемо ΔРТН - прямокутний.  ∠ТРН=120-90=30°Ю отже ТН=1/2РТ

РТ=2 ТН=6 см.

За теоремою Піфагора ТН=√(РТ²-ТН²)=√(36-9)=√27 см.

МК=РН=√27 см.

Розглянемо ΔКМТ - прямокутний. За теоремою Піфагора

МТ²=МК²+КТ²=27+36=63;  МТ=√63 см.