Помогите решить дифференциальное уравнение. Оно вроде простое, но у меня ответ вообще не тот получается(
Приложения:
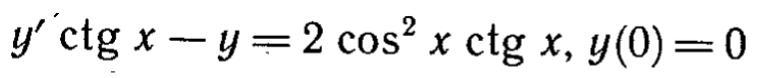
Ответы
Ответ дал:
1
Ответ:
Пошаговое объяснение:
1. Решаем однородное уравнение
y'ctg x-y=0
y'/y=tgx
y=1/cos(x)
Общее решение ищем, как f(x)/cos(x)
(f'/cos(x))*ctg(x)=2cos^2(x)*ctg(x)
f'=2cos^3(x)=2(1-sin^2(x))cos(x)
Интегрируем, используя замену cos(x)dx=d(sin(x))
f=2sin(x)-2sin^3(x)/3+C
Ответ y=(2sin(x)-2sin^3(x)/3+C)/cos(x)
Из условия y(0)=0 следует, что С=0
Похожие вопросы
1 год назад
2 года назад
2 года назад
7 лет назад
7 лет назад
8 лет назад
8 лет назад