Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 1 и 2, и боковым ребром, равным 4.
Ответы
Ответ дал:
1
Ответ:
S=2S(os)+S(bok)=2+8√5 ed²
Пошаговое объяснение:
Приложения:
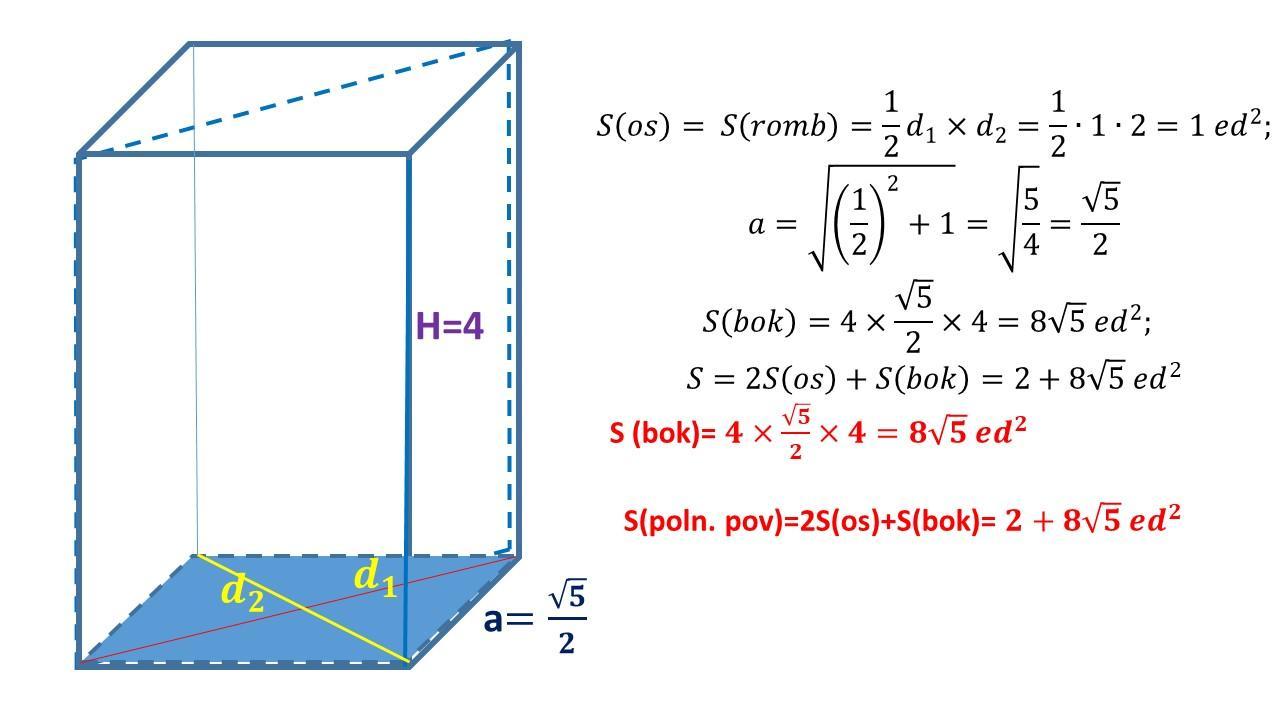
Ответ дал:
0
Ответ:
S полн.пов.=8√5+2
Пошаговое объяснение:
1) Найдем сторону основания по теореме Пифагора. Сторона ромба является гипотенузой, а половины диагоналей катетами, следовательно сторона основания
равна √0,5^2+1=√1,25=√5/2
2) Так как S полн.пов.=S бок.+2S осн.,
вычислим S бок.пов. и S осн.
S бок. пов.=Р*Н=(4*√5/2)*4=8√5
S осн.=1/2 произведения диагоналей
S осн.=(2*1)/2=1
S полн.пов.=8√5+2*1=8√5+2
Похожие вопросы
1 год назад
2 года назад
2 года назад
7 лет назад