Ответы
Ответ:
Объяснение: ЗАДАНИЕ 1
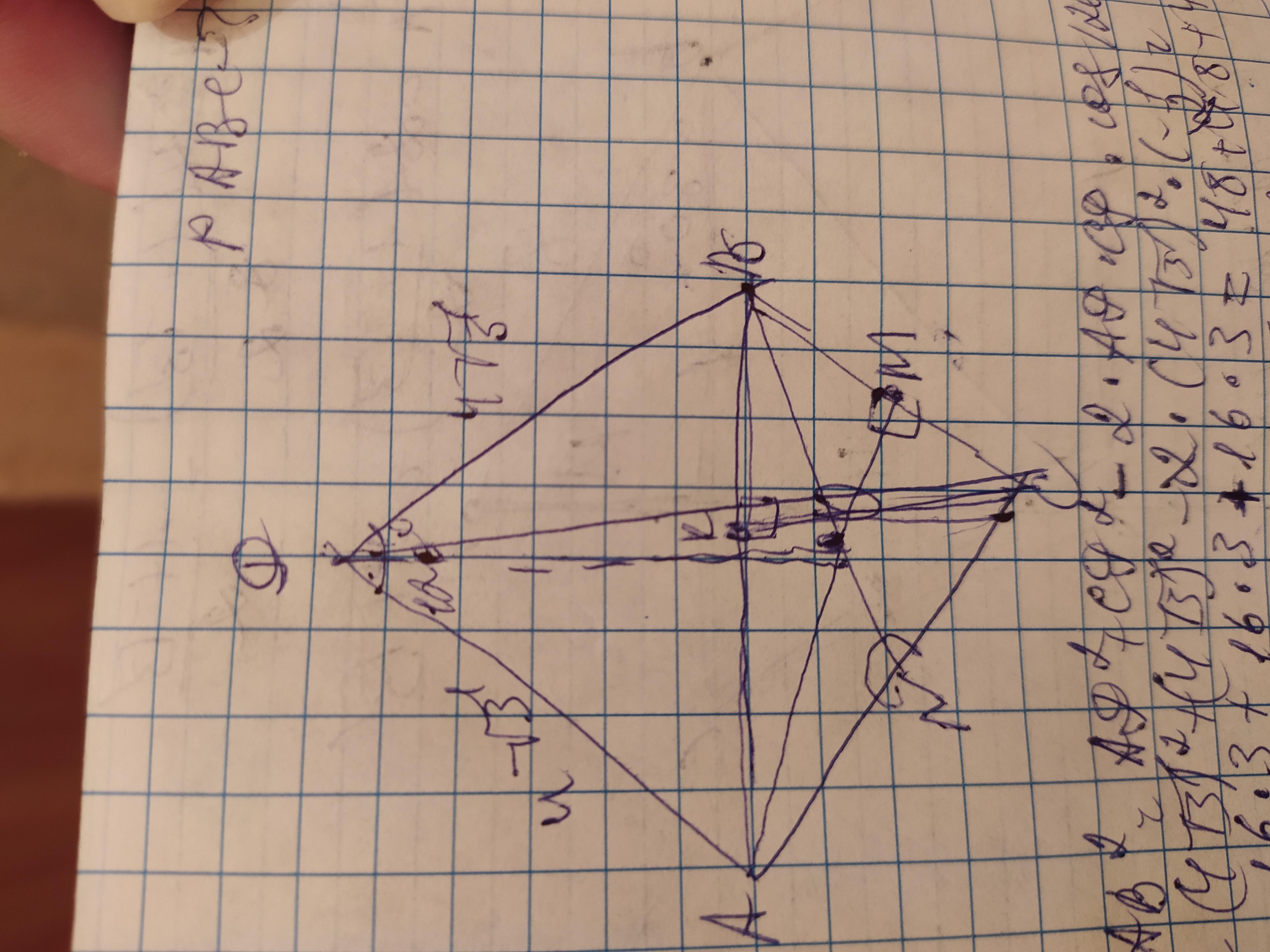
В основании правильной трёх угольной пирамиды лежит равносторонний треугольник, поэтому АВ=ВС=АС. Если АД=4√3, то СД и АД, то будут 4√3. Рассмотрим ∆АДВ. В нём боковые рёбра каждая по 4√3 и угол между ними 120°
Найдём сторону основания по теореме косинусов: АВ²=АД²+ВД²-2×АД×ВД×cos120°=
=(4√3)²+(4√3)²-2×4√3×4√3×(-½)=
=16×3+16×3-16×3=48+48+48=144;
АВ=√144=12
Периметр- это сумма всех сторон, поэтому: Р=12×3=36
ОТВЕТ: Р=36
ЗАДАНИЕ 2
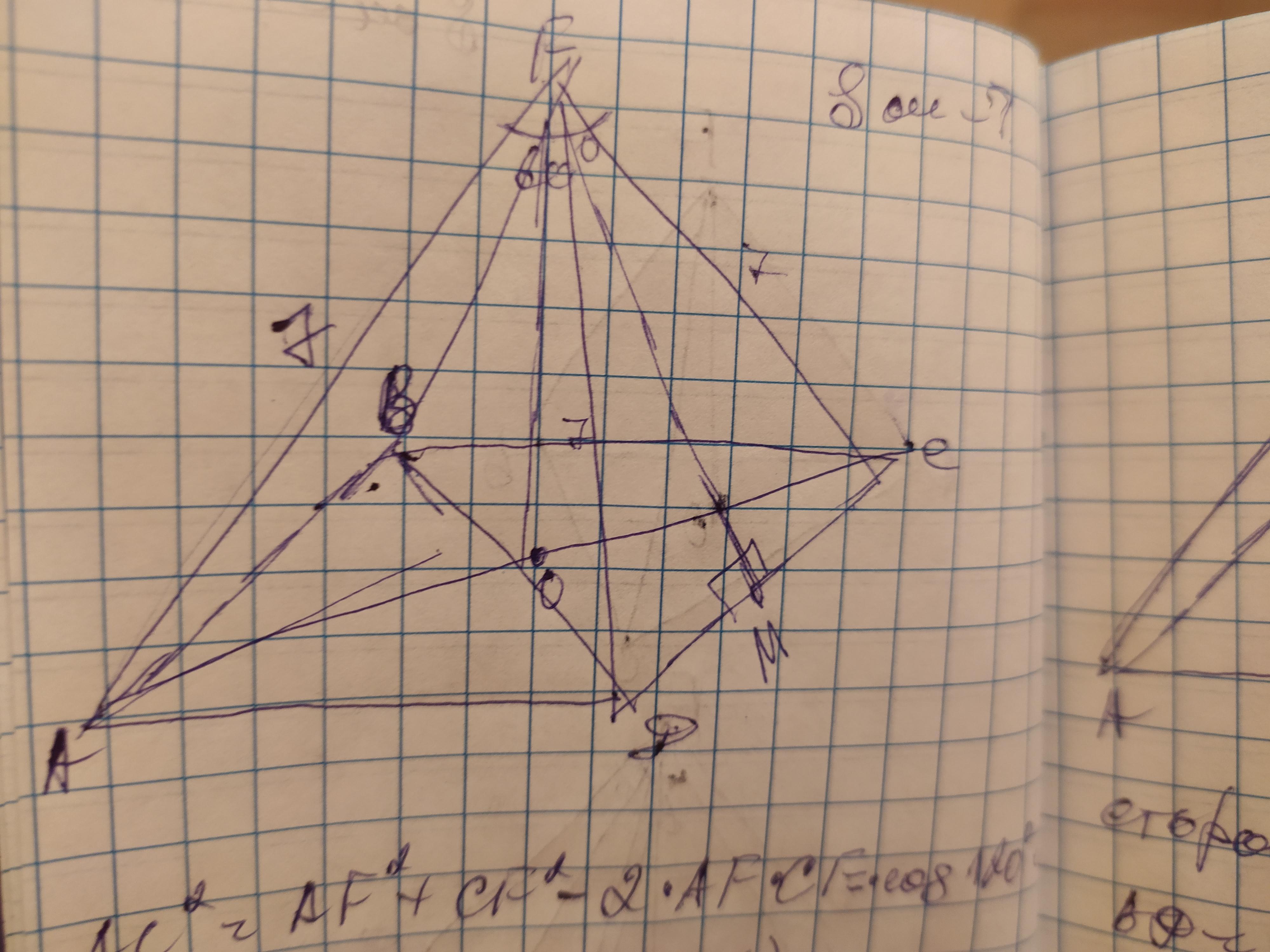
В основании правильной четырёхугольной пирамиды лежит квадрат поэтому АВ=ВС=СД=АД. Также все боковые рёбра тоже равны поэтому AF=BF=CF=ДF=7. Рассмотрим ∆AFC и в нём известны 2 стороны и угол между ними. Найдём диагональ АС по теореме косинусов:
АС²=AF²+CF²-2×AF×CF×cos60°=
=7²+7²-2×7×7×cos60°=49+49-2×49×½=49;
AC=√49=7
Диагональ АС делит квадрат на 2 равных равнобедренных прямоугольных треугольника, в которых стороны основания являются катетами а диагональ гипотенузой. В равнобедренном прямоугольном треугольнике катет меньше гипотенузы в √2 раз, поэтому АВ=ВС=СД=АД=7/√2
Теперь найдём площадь основания по формуле: S=a², где а - сторона основания
S=(7/√2)²=49/2=24,5(ед²)
ОТВЕТ: S=24,5(ед²)
ЗАДАНИЕ 3
В основании правильной четырёхугольной пирамиды лежит квадрат поэтому АВ=ВС=СД=АД
Так как известна площадь основания, то его сторона будет= √8
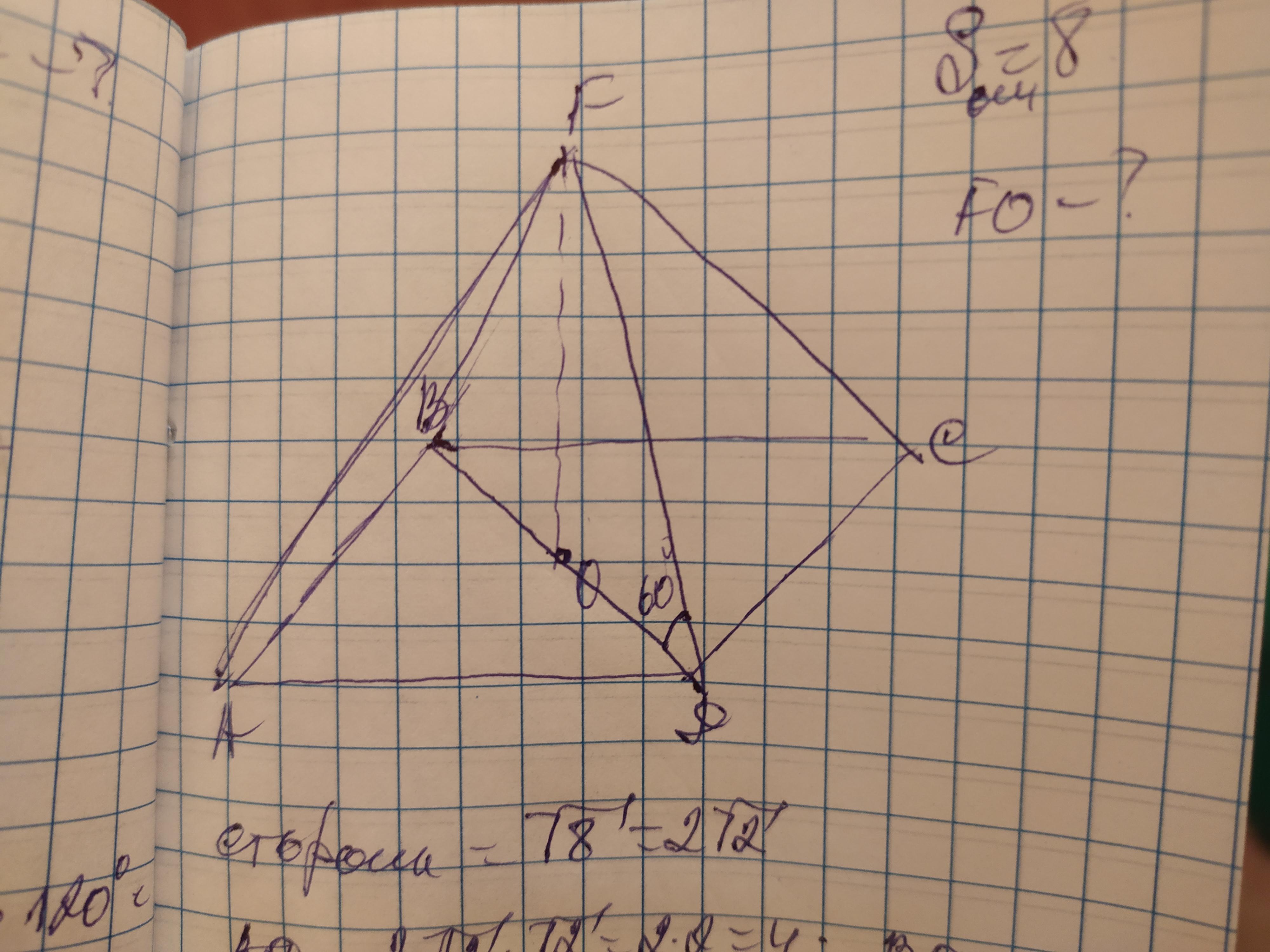
Диагональ ВД делит квадрат на 2 равных равнобедренных прямоугольных треугольника в которых стороны основания являются катетами а диагональ гипотенузой. Гипотенуза в равнобедренном прямоугольном треугольнике в √2 больше катета, поэтому ВД=АС=√8×√2=√16=4, тогда
ВО=ОД=4/2=2
Рассмотрим ∆FДО. Он прямоугольный где ДО и FO - катеты, а FД- гипотенуза. Угол Д=60°, и так как сумма острых углов прямоугольного треугольника составляет 90°, то угол ДFO=90-60=30°. Катет лежащий напротив него равен половине гипотенузы поэтому FД=ОД×2=
=2×2=4.
Теперь найдём высоту FO по теореме Пифагора: FO²=ДF²-ДО²=4²-2²=16-4=12
FO=√12=2√3
ОТВЕТ: высота FO=2√3