Предмет: Геометрия
Автор: onmyaccount
Вопрос задан 2 года назад

ПОМОГИТЕ ПЖ 90 баллов 1.В правильной треугольной пирамиде MABC боковое ребро = 3√2 см, а высота пирамиды = √6 см. Найдите площадь боковой поверхности пирамиды. 2. Даны точки (−1; −3; 2), (5; −1; −1), (3; 0; 2). а) Найдите координаты и модуль вектора ; б) Найдите координаты точки D, если = .

Iife20: Ду-Ау=АД; Ду-(-3)=3,7; Ду+3=3,7; Ду=3,7-3=0,7; Ду=0,7

Iife20: Дz-Az=АД; Dz-2=3,7; Dz=3,7+2=5,7; Dz=5,7

Iife20: Д(2,7; 0,7; 5,7)

Iife20: А точно ли ВА нужно найти, или может быть АВ?

Iife20: Не записывайте пока про точку Д

Iife20: Координаты ВС(3-5; 0-(-1); 2-(-1))=(-2; 0+1; 2+1)=(-2; 1; 3); ВС(-2; 1; 3). Есть теорема: равные векторы имеют равные координаты, поэтому если АД=ВС, то АД(-2; 1; 3). Теперь правильно, можете записывать

Iife20: Дх-Ах=АДх; Дх-(-1)=-2; Дх+1=-2; Дх=-2-1= -3

Iife20: Ду-Ау=АДу; Ду-(-3)=1; Ду+3=1; Ду=1-3= -2; Ду= -2

Iife20: Дz-Az=ADz; Dz-2=3; Dz=3+2=5; Dz=5

Iife20: Точка Д(-3; -2; 5)

Ответы

Ответ дал: Iife20

Ответ: Sбок.пов=27см²

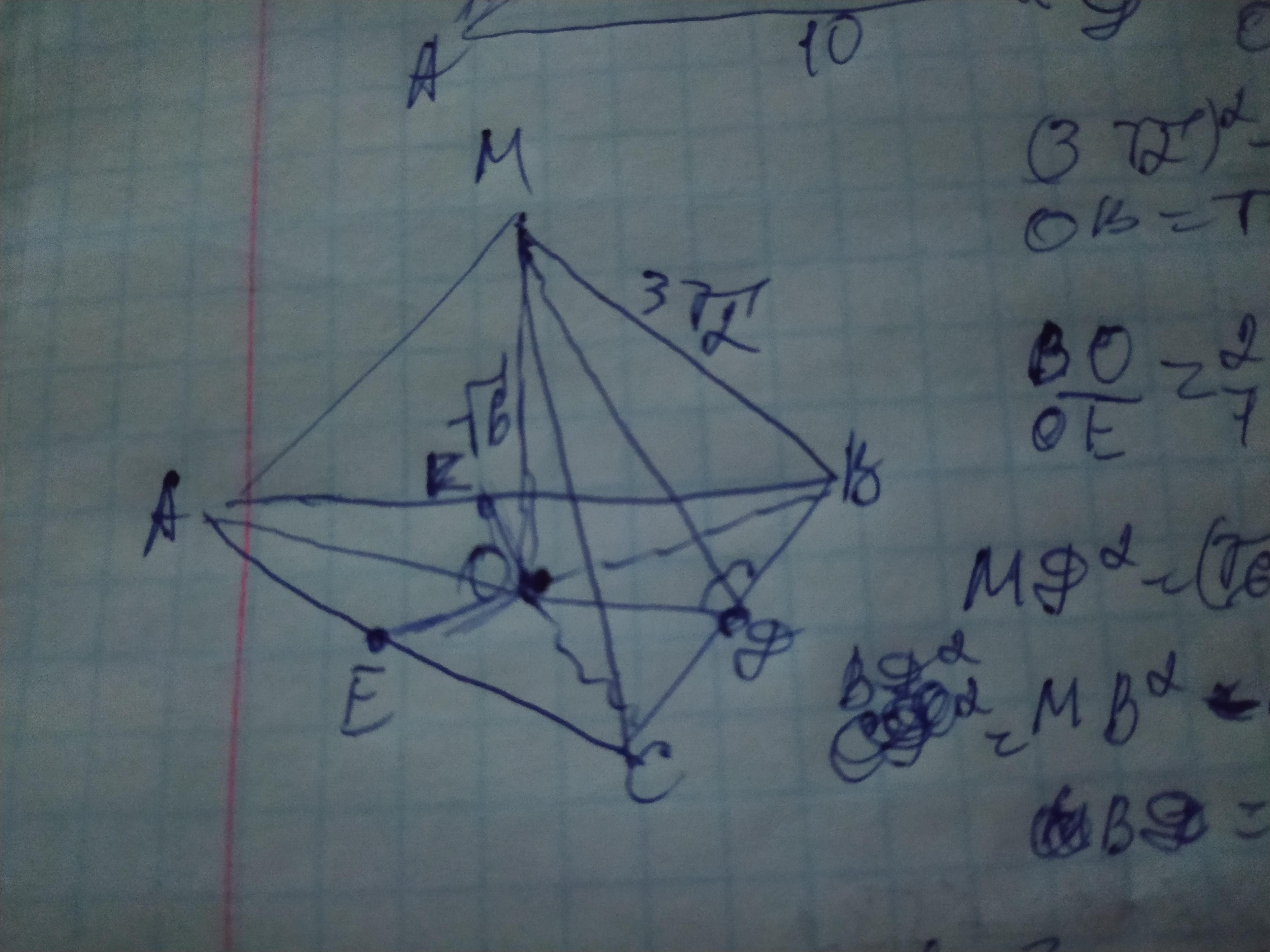
Объяснение: в основании правильной трёхугольной пирамиды лежит равносторонний треугольник. Проведём в нём высоты ДЕК, которые также являются биссектриса и и медианами основания. Отметим точку их пересечения О. Медианы при пересечении делятся в отношении 2: 1, начиная от вершины треугольника. Рассмотрим полученный ∆МОВ. Он прямоугольный и МО и ВО в нём являются катетами а ВМ- гипотенуза. Найдём ОВ по теореме Пифагора:

ВО²=МВ²-МО²=(3√2)²-(√6)²=9×2-6=18-6=12;

ВО=√12=2√3см

Так как ВО/ОЕ=2/1, то ОЕ=ОК=ОД=2√3/2=

=√3см

Также найдём МД в ∆МДО по теореме Пифагора: МД²=МО²+ДО²=(√6)²+(√3)³=

=6+3=9; МД=√9=3см

Теперь найдём сторону ВД в ∆СМВ по теореме Пифагора: ВД²=МВ²-МД²=

=(3√2)²-3²=9×2-9=18-9=9; ВД=√9=3см

Так как ∆СМВ равнобедренный (МВ=МС=3√2), то ВД=СД=3см. Следовательно ВС=3×2=6см

Теперь найдём площадь боковой грани СМВ по формуле:

Sбок.гр=½×BC×МД=½×6×3=9см².

Так как таких граней 3 то: