Предмет: Математика
Автор: paygildin02
Вопрос задан 2 года назад

Найдите,сумму,разность,произведение, частное комплексных чисел z1=1-2i,z2=-1+i

Приложения:

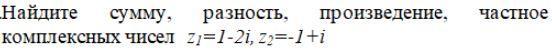
orjabinina: z1+z2= 1-2i +( -1+i )=-i

orjabinina: z1-z2= 1-2i -( -1+i )=2-3i

orjabinina: z1*z2=( 1-2i) *( -1+i )=-1 +3i-2i²=-1+3i+2=1+3i

orjabinina: z1/ z2=( 1-2i) /( -1+i )=( домножим и числитель и знаменатель на (i+1) , получим) =(-i+3)/(i²-1)=(-i+3)/(-2) . Вроде так

Ответы

Ответ дал: MathDaddy

$z1 = 1 - 2i \\ z2 = - 1 + i$

Сумма:

$z1 + z2 = 1 - 2i - 1 + i = - i$

Разность:

$z1 - z2 = 1 - 2i + 1 - i = 2 - 3i$

Произведение:

$z1 \times z2 = (1 - 2i)( - 1 + i) = \\ = - 1 + i + 2i - 2 {i}^{2} = - 1 + 3i + 2 = \\ = 1 + 3i$

Частное:

$\frac{z1}{z2} = \frac{ 1 - 2i}{ - 1 + i} = \frac{(1 - 2i)( - 1 - i)}{( - 1 + i)( - 1 - i)} = \\ = \frac{ - 1 + 2i - i + 2 {i}^{2} }{1 - i + i - {i}^{2} } = \frac{ - 3 + i}{2} = \\ = - \frac{3}{2} + \frac{1}{2} i = - 1.5 + 0.5i$

Похожие вопросы

Русский язык

1 год назад

расставьте ударения гуру, ракушка

Математика

1 год назад

скількома способами з 10 гравців в волейбольній команді можна вибрати стартову шістку

Математика

2 года назад

Найди делимое, выполнив необходимые действия. ________:7296=3(ост 727)

Русский язык

2 года назад

Спиши, вставляя пропущенные буквы. Подчеркни глаголы,которые употреблены в переносном значении. З...леном морем хлынет лето, Луга рамашкой еаведнит, И коромыслом с...мицветным, В бездонном небе

Химия

7 лет назад

Кр з хімії 8 клас дам 50 балів!

Геометрия

7 лет назад

решите, пожалуйста даю 35 баллов срочно

Алгебра

8 лет назад

Номер 6 срочно плизз

Математика

8 лет назад

Если человек родился 2002 года а др 20 августа то сколько ему лет?