Ответы
Ответ:
Пошаговое объяснение:
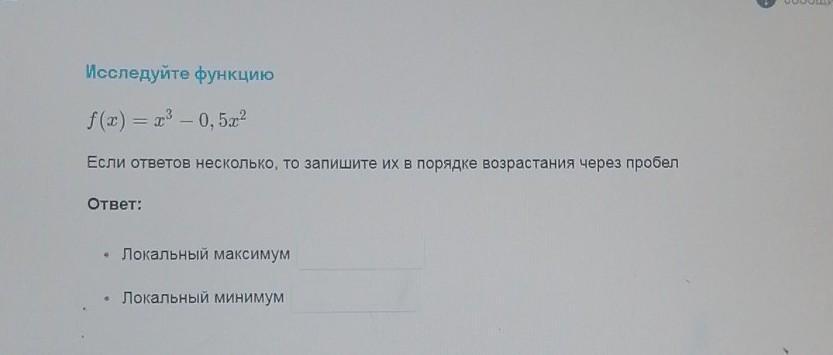
f(x) = x³ - 0.5 x²
исследование на экстремумы проводится при помощи производной
необходимое условие наличия точек экстремума f'(x) = 0 в этих точках
ну и найдем эти точки
f'(x) = (x³)' - 0.5 (x²)' = 3x² - x
3x² - x = 0; x(3x-1) = 0 ⇒ x₁ = 0 ; x₂ = 0.333
значение функции в этих точках
f(0) = 0
f(0.333) = -0.0185
теперь посмотрим на достаточное условие экстремума функции. оно применяется при помощи второй производной
если в точке х₀
f''(x₀) > 0 , то точка x₀ - точка локального (глобального) минимума
если в точке х₀
f''(x₀) < 0 , то точка x₀ - локальный (глобальный) максимум.
вот и посмотрим
f''(x) = 6x-1
f''(0) = -1 < 0 - значит точка x = 0 точка максимума функции.
f''(0.333) = 1 > 0 - значит точка x = 0.333 точка минимума функции.
значение функции в этих точках
f(0) = 0
f(0.333) = -0.0185