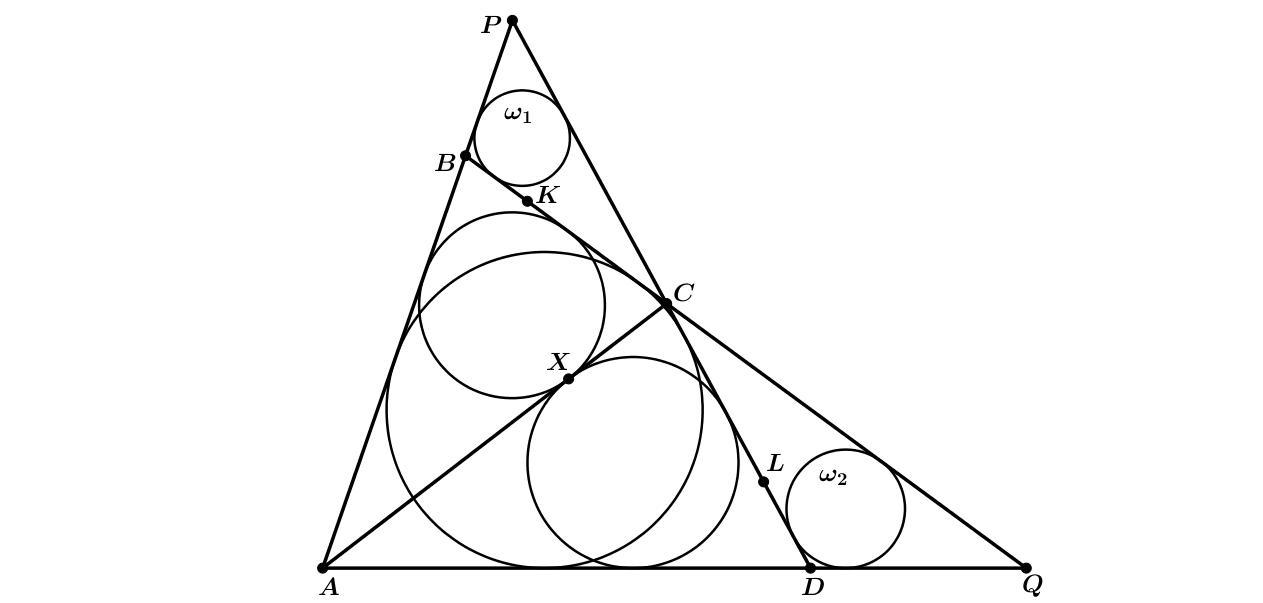
Дан описанный четырёхугольник ABCD. P и Q — точки пересечения прямых AB и CD, AD и BC. Вписанные окружности треугольников ABC и ACD касаются диагонали AC в точке X. Окружности ω1 и ω2 вписаны в треугольники PBC и QCD. Точки K и L — основания биссектрис углов P и Q треугольников PBC и QCD. Общие внешние касательные к ω1 и ω2 пересекаются в точке O. Какие тройки точек лежат на одной прямой?
Приложения:
Ответы
Ответ дал:
3
Ответ:
OPQ, KLO
Объяснение:
не спрашивай, я угадала)))
lover2010:
да ты мегамозг :D
ахаха я просто мастер угадывать ответы >_
Похожие вопросы
1 год назад
1 год назад
2 года назад
7 лет назад
7 лет назад