Найти тангенс угла наклона касательной

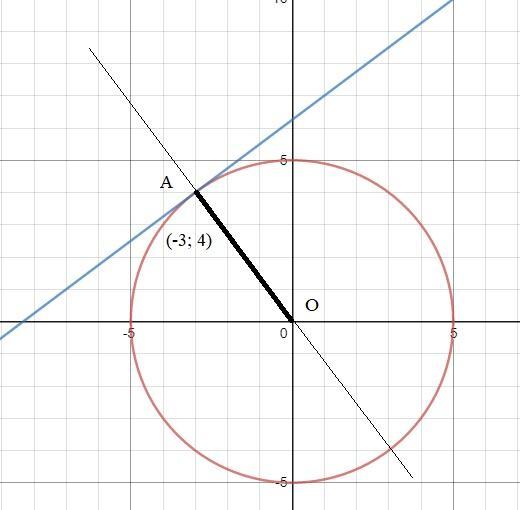
Касательная перпендикулярна радиусу, проведенному в точку касания.

Составим уравнение прямой, содержащей радиус.

Эта прямая  проходит через начало координат и точку (-3;4)

y=k₁x

4=k₁·(-3)

k₁= - 4/3

Произведение угловых коэффициентов взаимно перпендикулярных прямых k₁ ·k₂=-1

k₂=3/4

О т в е т. 3/4

Ответ:

0,75

Пошаговое объяснение:

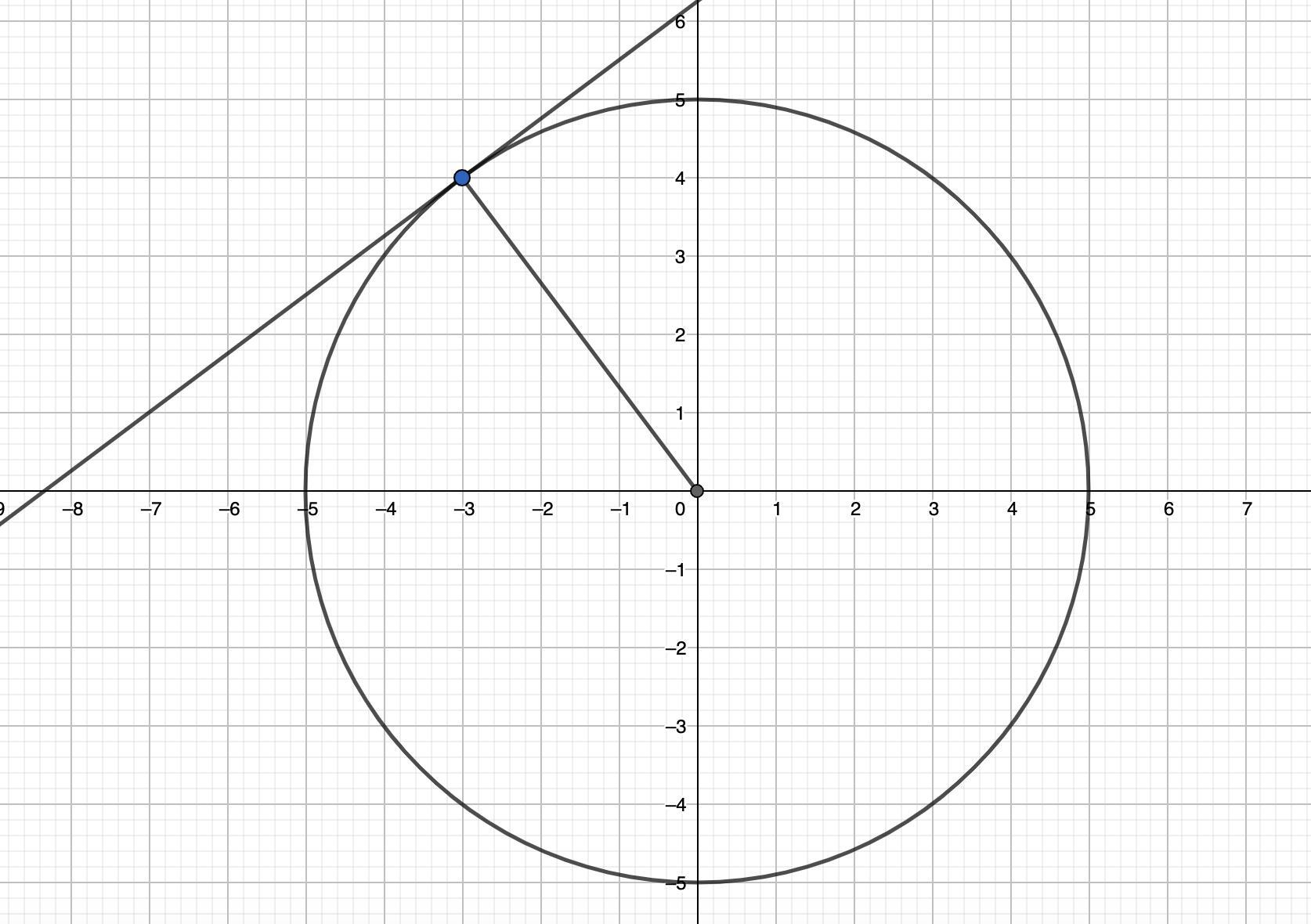
Чтобы найти тангенс угла наклона касательной, необходимо найти коэффициент перед x в уравнении касательной.

Проведём радиус в точку касания. Он лежит на прямой . Действительно, точки (0; 0) и (-3; 4) ей принадлежат. Касательная перпендикулярна радиусу, значит, коэффициент перед x равен .