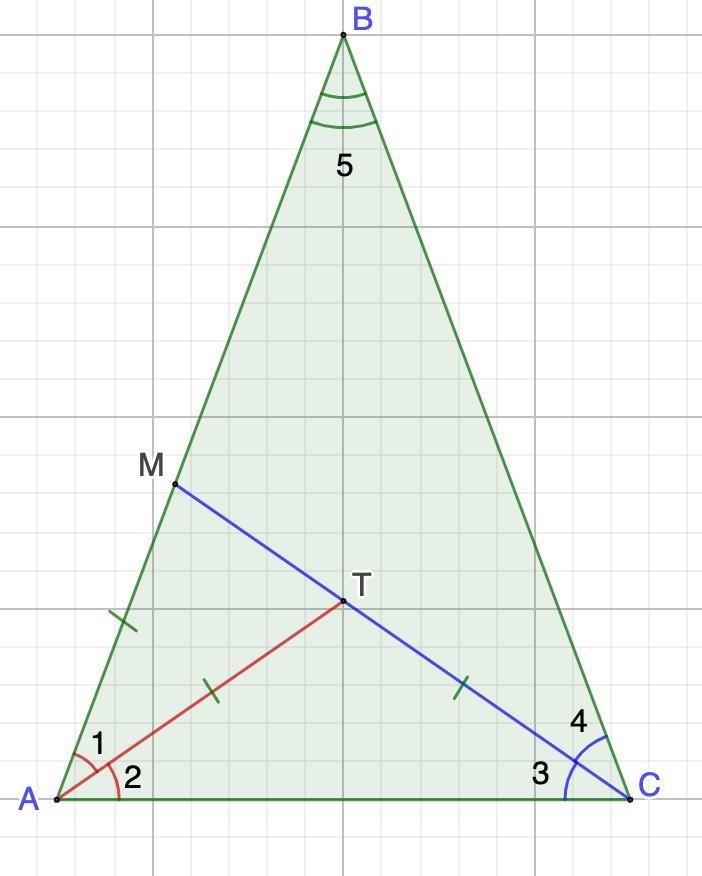
В треугольнике ABC биссектриса угла С пересекает сторону AB в точке М, а биссектриса угла A пересекает отрезок CM в точке Т. Оказалось что отрезки CM и AT разбили треугольник на три равнобедренных треугольника. Найдите углы треугольник ABC

Ответ:

∠А = 72°;

∠В = 36°;

∠С = 72°.

Объяснение:

Дано: ΔАВС;

СМ - биссектриса ∠С;

АТ - биссектриса ∠А;

ΔМАТ; ΔАТС; ΔВМС - равнобедренные.

Найти: ∠А; ∠В; ∠С.

Решение:

Рассмотрим углы:

∠1=∠2 (АТ - биссектриса ∠А)

• В равнобедренном треугольнике углы при основании равны.

∠2 =∠3 (ΔАТС - равнобедренный)

∠3 =∠4 (СМ - биссектриса ∠С)

∠4 =∠5 (ΔМВС - равнобедренный)

⇒ ∠1 = ∠2 = ∠3 = ∠4 = ∠5

Пусть ∠1 = ∠2 = ∠3 = ∠4 = ∠5 = α

• Сумма углов треугольника равна 180°.

⇒ ∠А + ∠В + ∠С = (∠1 + ∠2) + (∠3 + ∠4) + ∠5 = 5α = 180°

5α = 180°   |:5

α = 36°

Найдем углы треугольника:

∠А = ∠1 + ∠2 = 72°;

∠В = 36°;

∠С =∠3 +∠4 = 72°.

⇒ ∠А = 72°; ∠В = 36°; ∠С = 72°.