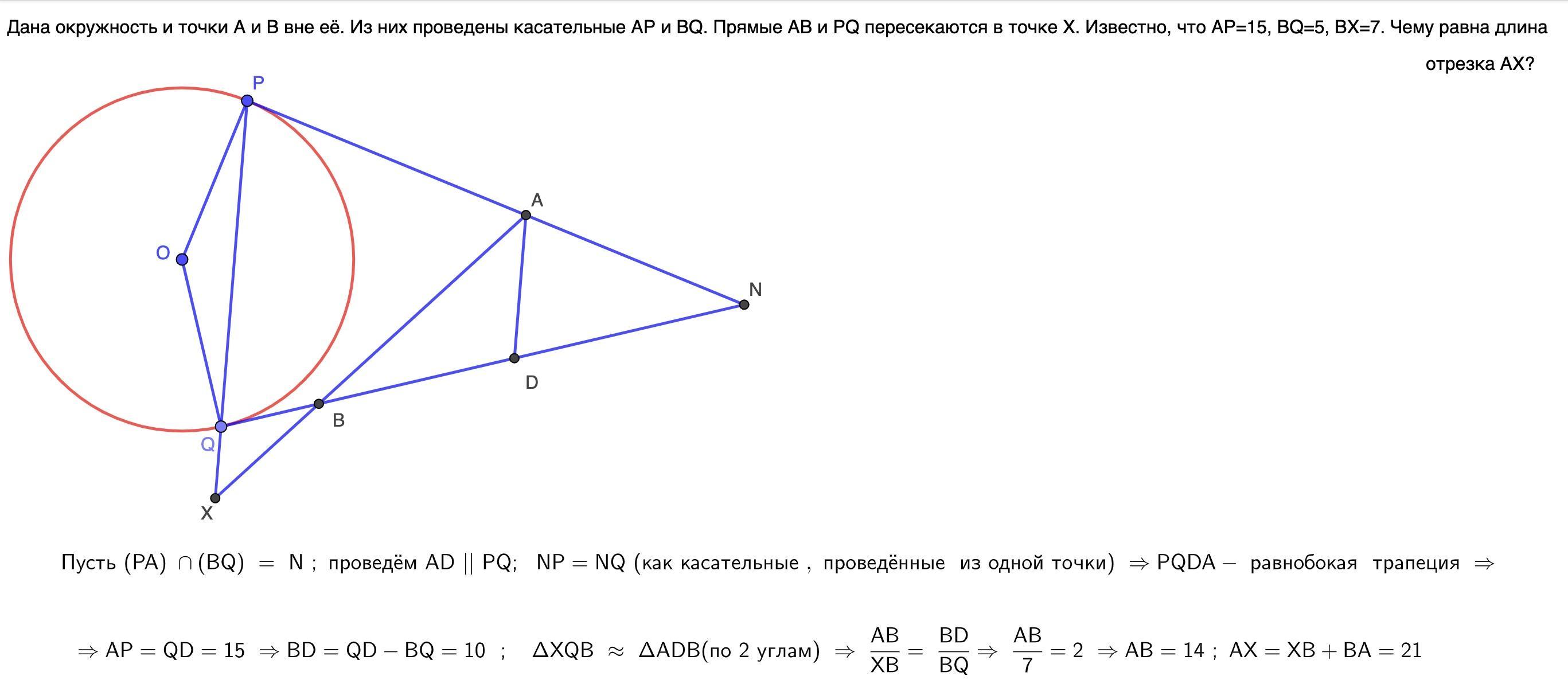
Дана окружность и точки A и B вне её. Из них проведены касательные AP и BQ. Прямые AB и PQ пересекаются в точке X. Известно, что AP=15, BQ=5, BX=7. Чему равна длина отрезка AX?

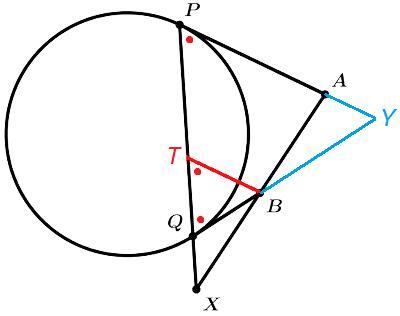
Продлим PA и QB до пересечения в точке Y.

Отрезки касательных из одной точки равны, △PYQ - равнобедренный, APQ=BQP.

Проведем BT||AP.

BTQ=APQ=BQP, △TBQ - равнобедренный, BT=BQ

△BXT~△AXP => BX/AX =BT/AP => 7/AX =5/15 => AX=21

Или

sin(P) =sin(BQP) =sin(BQX)

Теорема синусов

AX/sin(P) =AP/sin(X)

BX/sin(BQX) =BQ/sin(X)

AX/BX =AP/BQ

Ответ:

21

Объяснение: