Докажите, что если квадрат одной медианы треугольника равен одной пятой суммы квадратов двух других медиан, треугольник прямоугольный
Аноним:
Доказательство через векторы подойдет?
Ответы
Ответ дал:
0
Дано: Ma^2 +Mb^2 =5 Mc^2
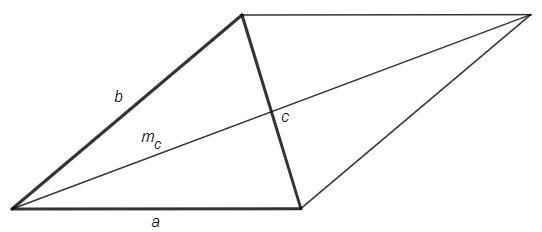
Достроим произвольный треугольник до параллелограмма.
По свойству диагоналей
4Mc^2 +c^2 =2(a^2 +b^2)
Аналогично для медиан Ma и Mb.
Отсюда в произвольном треугольнике
Ma^2 +Mb^2 +Mc^2 =3/4 (a^2 +b^2 +c^2)
Вычитая условие, получим
8Mc^2 = a^2 +b^2 +c^2
Приравняем по Mc^2
(2a^2 +2b^2 -с^2)/4 =(a^2 +b^2 +c^2)/8 <=> a^2 +b^2 =c^2
Приложения:
Помогите пожалуйста https://znanija.com/task/37930911
Похожие вопросы
1 год назад
1 год назад
2 года назад
7 лет назад
7 лет назад
8 лет назад
8 лет назад