Предмет: Математика
Автор: Katie004
Вопрос задан 2 года назад

Помогите с задачей, пожалуйста!

Перевод задачи:

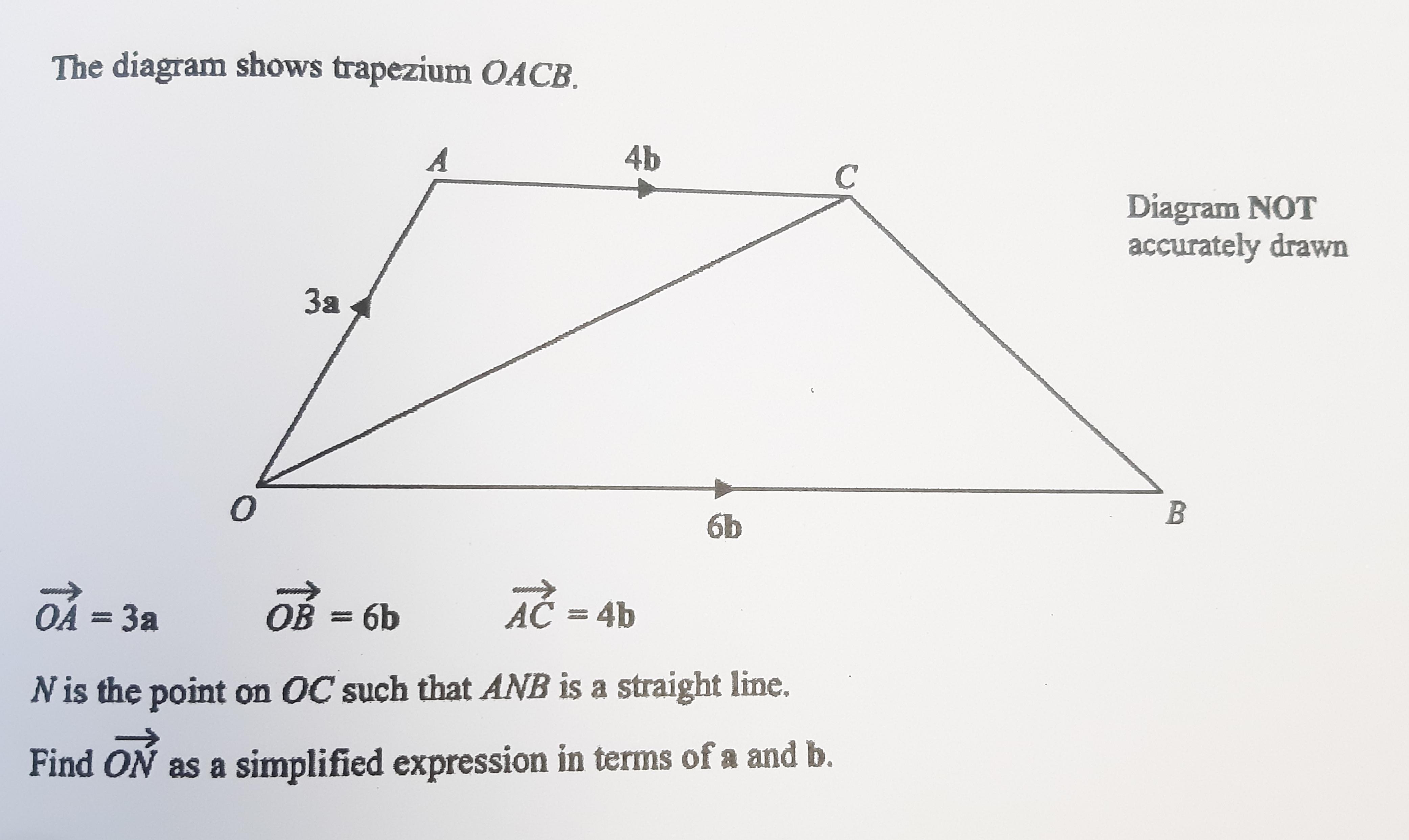
На рисунке ОАСВ — трапеция.

Вектор ОА= 3а, вектор ОВ= 6b, вектор АС= 4b.

N — это такая точка ОС, что ANB является прямой линией.

Выразите вектор ON через a и b, в ответе записать упрощённое выражение.

Приложения:

Vopoxov: ...Это, как его - а! Прриветствую! Я верно понял из условия, что нам дана трапеция, где сторонами являются векторы?

Vopoxov: ...а если говорить проще, то N - это ни что иное, как точка пересечения диагоналей этой самой трапеции?

Vopoxov: Откуда задачко, если не секрет?

Katie004: Здравствуйте, задача про векторы по британской программе 11 класса, оксфордская школа.

Ответы

Ответ дал: sharofat0

Ответ:

вектор ON= вектор 1,8а+

+вектор 2,4b

Выразить вектор ОN через а и b.

Приложения:

Vopoxov: Однако результаты у нас с вами совпали:). Думаю, это не просто совпадение!)

Katie004: Спасибо большое за решение!!

Ответ дал: Vopoxov

Ответ:

$\overrightarrow {ON} = 1.8a + 2.4b$

Пошаговое объяснение:

ОАСВ — трапеция

Очевидно, что векторы АС и ОВ коллинеарны, поэтому АС и ОВ параллельны. Поэтому:

АС и ОВ - основания трапеции

ОА и СВ - боковые стороны,

OC - диагональ трапеции. Вектор ОС равен сумме векторов:

$\overrightarrow {OC} = \overrightarrow {OA} + \overrightarrow {AC} = 3a+4b \:$

N — тчк на ОС, такая, что ANB - прямая линия.

Если по-русски, то фраза значит банальное:

"Диагонали трапеции пересекаются в т. N"

Далее рассматриваем треугольники

АСN и BON - они подобные, с коэффициентом подобия

ON / CN = 6 /4 = 1,5

N - т. пересечения диагоналей, а значит вектор ОС можно рассматривать также как сумму векторов ON и NC

$\overrightarrow {OC} = \overrightarrow {ON} + \overrightarrow {NC} = 3a+4b$

Причем заметим, что ОС ОN и NC - коллинеарны, т.е

$\overrightarrow {OC} = k \cdot \overrightarrow {ON} = n \cdot \overrightarrow {NC}$

где k, n - некоторые коэффициенты

А ведь мы ж знаем, что

$\overrightarrow {ON} = 1.5 \cdot \overrightarrow {NC} = > \\ \overrightarrow {OC} = \overrightarrow {ON} + \overrightarrow {NC} \\ \overrightarrow {OC} = (1.5 \cdot \overrightarrow {NC} )+ \overrightarrow {NC} \\ \overrightarrow {OC} = 2.5 \cdot\overrightarrow {NC} = > \\ = > \overrightarrow {NC} = \frac{ \overrightarrow {OC} }{2.5} = 0.4 \cdot\overrightarrow {OC}$

А отсюда выразим вектор ON:

$\overrightarrow {ON} = 1.5 \cdot \overrightarrow {NC} \\ \overrightarrow {ON} = 1.5 \cdot (0.4 \cdot\overrightarrow {OC}) = 0.6 \cdot\overrightarrow {OC}$