Предмет: Алгебра
Автор: vladgujjvan0
Вопрос задан 2 года назад

< >

Найти общее решение дифференциального уравнения. Под цифрой 3. Не через калькулятор и как можно подробнее.

Приложения:

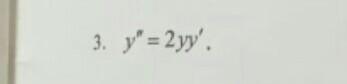
vladgujjvan0: y''=2yy'

Ответы

Ответ дал: Artem112

2

$y''=2yy'$

Это дифференциальное уравнение второго порядка, допускающее понижение порядка, так как оно не содержит в своей записи переменную $x$ .

Замена:

$y'=p$

$\Rightarrow y''=p'=\dfrac{dp}{dx}=\dfrac{dp}{dy}\cdot\dfrac{dy}{dx} =y'\cdot\dfrac{dp}{dy}= p\cdot\dfrac{dp}{dy}$

Получим уравнение:

$p\cdot\dfrac{dp}{dy}=2yp$

Если $p=0$ , то есть $y'=0$ , то $\boxed{y=C}$

Если $p\neq 0$ , то:

$\dfrac{dp}{dy}=2y$

$dp=2ydy$

$\int dp=\int 2ydy$

$p=y^2+C_1$

Обратная замена:

$y'=y^2+C_1$

$\dfrac{dy}{dx} =y^2+C_1$

$\dfrac{dy}{y^2+C_1} =dx$

$\int\dfrac{dy}{y^2+C_1} =\int dx$

$\boxed{\dfrac{1}{\sqrt{C_1}}\mathrm{arctg}\dfrac{y}{\sqrt{C_1}} =x+C_2}$ - общий интеграл уравнения

Выразим функцию в явном виде:

$\mathrm{arctg}\dfrac{y}{\sqrt{C_1}} =x\sqrt{C_1}+C_2\sqrt{C_1}$

$\dfrac{y}{\sqrt{C_1}} =\mathrm{tg}\left(x\sqrt{C_1}+C_2\sqrt{C_1}\right)$

$\boxed{y=\sqrt{C_1}\cdot\mathrm{tg}\left(x\sqrt{C_1}+C_2\sqrt{C_1}\right)}$

vladgujjvan0: Здравствуйте, добавил два вопроса по дифференциальным уравнениям, решите пожалуйста.

Похожие вопросы

Физика

1 год назад

люди добрые помогите!

Английский язык

1 год назад

the children still (to play) in the garden when their mother (to come back)from work

Другие предметы

2 года назад

нужны срочно фамилии мастеров корабелов в городце в 19 в

Окружающий мир

2 года назад

перечисли несколько правил и норм здорового питания которых должен придерживаться каждый человек

Геометрия

7 лет назад

даю 35 помогите сторона правильного шестикутника вписаного в коло дорівнює 4 см .знайти площу квадрата описаного навколо цього кола

Математика

7 лет назад

Ребята пожалуйста подскажите

История

8 лет назад

что здесь написано по финикийски? 1. н крст 2. н лгт 3.н бвт члвк 4. пчтт тц мт

Математика

8 лет назад

начертить отрезок4/5 длины,которго равны длине отрезка АБ