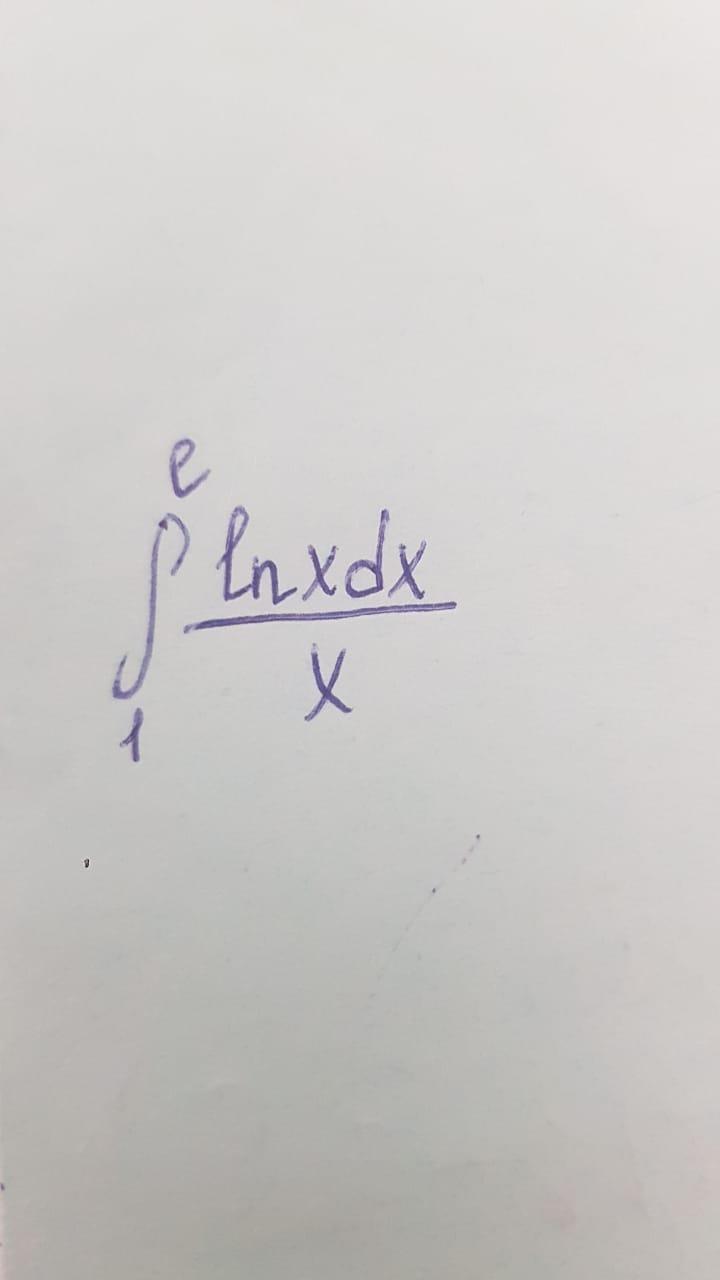Решите определенный интеграл

Приложения:

Ответы

Ответ дал: sangers1959

Объяснение:

$\int\limits^e_1 {\frac{lnx}{x} } \, dx.\\$

Вычислим вначале неопределённый интеграл:

$\int\limits {\frac{lnx}{x} } \, dx$

Пусть u=lnx ⇒ du=(lnx)'=dx/x.

$\int\limits {\frac{lnx}{x} } \, dx =\int\limits {u} \, du=\frac{u^2}{2}=\frac{ln^2x}{2}\ \ \ \ \Rightarrow\\\frac{ln^2x}{2}\ |_1^e=\frac{ln^2e}{2}-\frac{ln^21}{2}= \frac{1^2}{2}-\frac{0^2}{2}=\frac{1}{2}-0=\frac{1}{2}=0,5.$

$\int\limits^e_1 {\frac{lnx}{x} } \, dx=0,5.$

Похожие вопросы

Русский язык

1 год назад

помогитеееееееееееееееее

Литература

1 год назад

Пожалуйста ооочень краткий и понятный пересказ,, Барышня-крестьянка'' Умоляю Только не длинно.

Русский язык

2 года назад

пожалуйста помогите написать составит 4предложения и выделить в них корень суфикс окончание и основу .задания 2класса

Английский язык

2 года назад

Помогите написать сочинение о известном человеке в СМИ на английском

Физика

7 лет назад

Физика,помогите пожалуйста!

Литература

7 лет назад

Сент- Экзэпеори « маленький принц» кем стал главный герой когда вырос варианты ответа путешествинеком лётчикам учителем

Математика

8 лет назад

Вычислите: 10-3 4/5 - 5 2/3

Математика

8 лет назад

продумайте задачу про класс из 33 учебников.Помогите пожалуста.даю 60 баллов