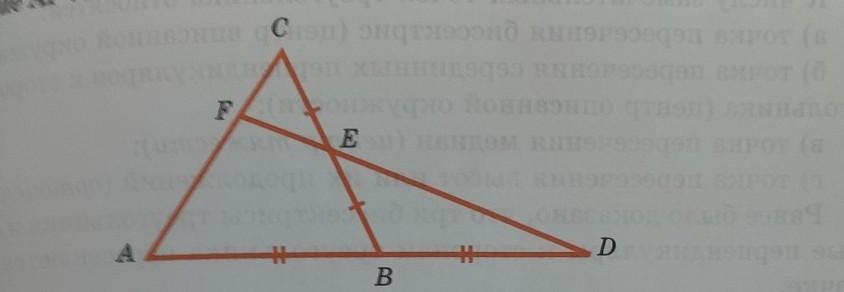
Помогите пожалуйста! На продолжении стороны AB треугольника ABC взята точка D, AB=BD .через нее середину E стороны BC проведена прямая пересекающая сторону AC в точке F. Найдите соотношение AF:FC .​

Ответ:

Объяснение:

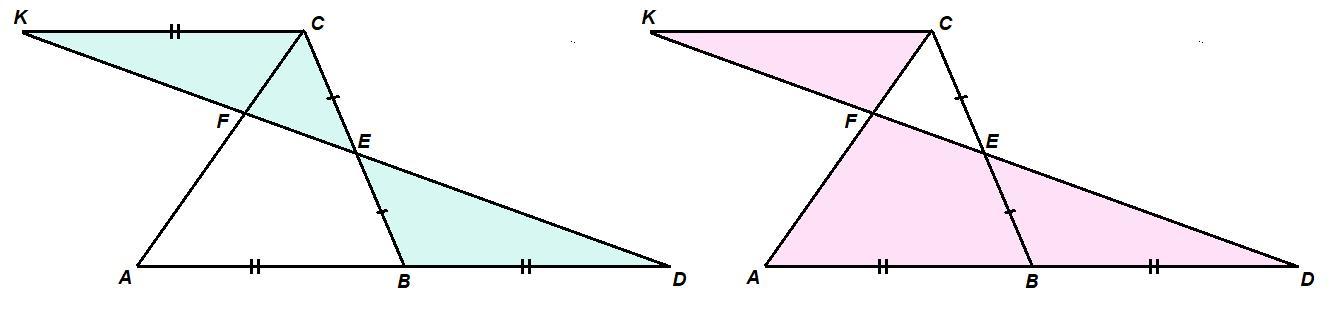
Из вершины С проведем прямую СК║АВ. К - точка пересечения СК и DF.

ΔКСЕ = ΔDBE по стороне и двум прилежащим к ней углам:

• CE = EB по условию;
• углы при вершине Е равны как вертикальные;
• ∠КСЕ = ∠DBE как накрест лежащие при пересечении параллельных прямых СК и АВ секущей CB.

Значит, СК = AB = BD.

ΔKCF ~ ΔDAF по двум углам:

• углы при вершине F равны как вертикальные;
• ∠KCF = ∠DAF как накрест лежащие при пересечении параллельных прямых СК и АВ секущей CА.