Дан равносторонний треугольник ABC, периметр которого равен 18. Найдите (BC-3BA)^2

Ответ:

252 ед².

Объяснение:

В равностороннем треугольнике стороны равны, а все углы по 60°.

ВА = ВС = АС = 18:3 = 6 ед.

Вектор (ВС - 3ВА)² - это квадрат модуля вектора |ВС - 3ВА|.

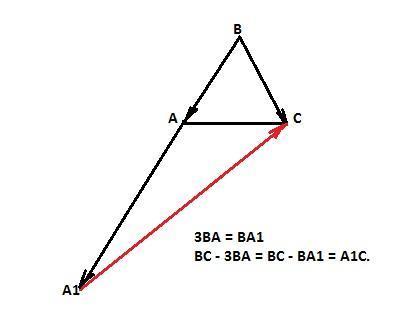
Вектор 3ВА= ВА1 = 18 ед.  (равен трем коллинеарным векторам ВА, расположенным на одной прямой, конец которого будет в точке А1).

По правилу вычитания векторов имеем:

ВС - 3ВА = ВС - ВА1 = А1С.

Вектор А1С² находим по теореме косинусов:

|A1С|² = |BC|² + |BA1|² - 2|BC|·|BA1|·Cos60 =>

|A1С|² = |6|² + |18|² - 2·6·18·(1/2) = 252 ед.

Но А1С² это как раз искомый вектор.