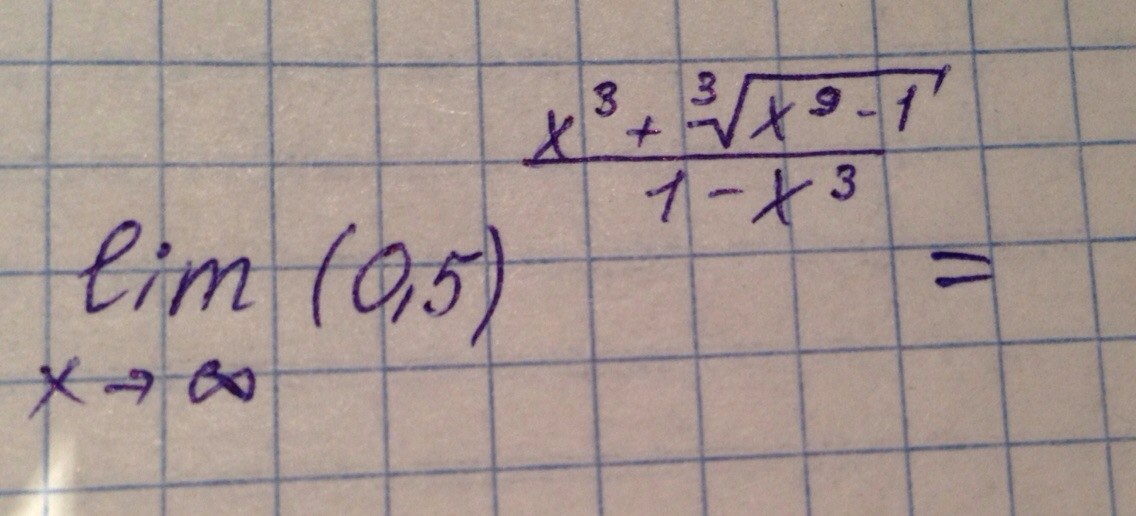Ответы
Ответ дал:
0
В силу непрерывности показательной функции возможен предельный переход в степени. То есть
![lim_{x to infty} 0,5^frac{x^3+sqrt[3]{x^9-1}}{1-x^3} =0,5^{ lim_{x to infty}frac{x^3+sqrt[3]{x^9-1}}{1-x^3}}= lim_{x to infty} 0,5^frac{x^3+sqrt[3]{x^9-1}}{1-x^3} =0,5^{ lim_{x to infty}frac{x^3+sqrt[3]{x^9-1}}{1-x^3}}=](https://tex.z-dn.net/?f=+lim_%7Bx+to+infty%7D+0%2C5%5Efrac%7Bx%5E3%2Bsqrt%5B3%5D%7Bx%5E9-1%7D%7D%7B1-x%5E3%7D+%3D0%2C5%5E%7B+lim_%7Bx+to+infty%7Dfrac%7Bx%5E3%2Bsqrt%5B3%5D%7Bx%5E9-1%7D%7D%7B1-x%5E3%7D%7D%3D)
Поделим дробь и числитель и знаменатель на
Напишем для простоты только степень
![lim_{x to infty} frac{x^3+sqrt[3]{x^9-1}}{1-x^3}= lim_{x to infty} frac{frac{x^3+sqrt[3]{x^9-1}}{x^3}}{frac{1-x^3}{x^3}}= lim_{x to infty} frac{x^3+sqrt[3]{x^9-1}}{1-x^3}= lim_{x to infty} frac{frac{x^3+sqrt[3]{x^9-1}}{x^3}}{frac{1-x^3}{x^3}}=](https://tex.z-dn.net/?f=+lim_%7Bx+to+infty%7D+frac%7Bx%5E3%2Bsqrt%5B3%5D%7Bx%5E9-1%7D%7D%7B1-x%5E3%7D%3D+lim_%7Bx+to+infty%7D+frac%7Bfrac%7Bx%5E3%2Bsqrt%5B3%5D%7Bx%5E9-1%7D%7D%7Bx%5E3%7D%7D%7Bfrac%7B1-x%5E3%7D%7Bx%5E3%7D%7D%3D)
![= lim_{x to infty} frac{1+frac{sqrt[3]{x^9-1}}{x^3}}{frac{1}{x^3}-1}= = lim_{x to infty} frac{1+frac{sqrt[3]{x^9-1}}{x^3}}{frac{1}{x^3}-1}=](https://tex.z-dn.net/?f=%3D+lim_%7Bx+to+infty%7D+frac%7B1%2Bfrac%7Bsqrt%5B3%5D%7Bx%5E9-1%7D%7D%7Bx%5E3%7D%7D%7Bfrac%7B1%7D%7Bx%5E3%7D-1%7D%3D)
Заметим, что слагаемое в знаменателе при
в знаменателе при  стремиться к нулю, то есть
стремиться к нулю, то есть
![= lim_{x to infty} frac{1+frac{sqrt[3]{x^9-1}}{x^3}}{-1}= lim_{x to infty}(-(1+frac{sqrt[3]{x^9-1}}{x^3}))= = lim_{x to infty} frac{1+frac{sqrt[3]{x^9-1}}{x^3}}{-1}= lim_{x to infty}(-(1+frac{sqrt[3]{x^9-1}}{x^3}))=](https://tex.z-dn.net/?f=%3D+lim_%7Bx+to+infty%7D+frac%7B1%2Bfrac%7Bsqrt%5B3%5D%7Bx%5E9-1%7D%7D%7Bx%5E3%7D%7D%7B-1%7D%3D+lim_%7Bx+to+infty%7D%28-%281%2Bfrac%7Bsqrt%5B3%5D%7Bx%5E9-1%7D%7D%7Bx%5E3%7D%29%29%3D)
![=- lim_{x to infty}(1+frac{sqrt[3]{x^9-1}}{x^3})=-1- lim_{x to infty}frac{sqrt[3]{x^9-1}}{x^3}= =- lim_{x to infty}(1+frac{sqrt[3]{x^9-1}}{x^3})=-1- lim_{x to infty}frac{sqrt[3]{x^9-1}}{x^3}=](https://tex.z-dn.net/?f=%3D-+lim_%7Bx+to+infty%7D%281%2Bfrac%7Bsqrt%5B3%5D%7Bx%5E9-1%7D%7D%7Bx%5E3%7D%29%3D-1-+lim_%7Bx+to+infty%7Dfrac%7Bsqrt%5B3%5D%7Bx%5E9-1%7D%7D%7Bx%5E3%7D%3D)
Занесем под корень
под корень
![=-1- lim_{x to infty}sqrt[3]{frac{x^9-1}{x^9}}}=-1- lim_{x to infty}sqrt[3]{1-frac{1}{x^9}}}= =-1- lim_{x to infty}sqrt[3]{frac{x^9-1}{x^9}}}=-1- lim_{x to infty}sqrt[3]{1-frac{1}{x^9}}}=](https://tex.z-dn.net/?f=%3D-1-+lim_%7Bx+to+infty%7Dsqrt%5B3%5D%7Bfrac%7Bx%5E9-1%7D%7Bx%5E9%7D%7D%7D%3D-1-+lim_%7Bx+to+infty%7Dsqrt%5B3%5D%7B1-frac%7B1%7D%7Bx%5E9%7D%7D%7D%3D)
Заметим, что слагаемое под корнем при
под корнем при  стремиться к нулю, то есть
стремиться к нулю, то есть
![=-1- lim_{x to infty}sqrt[3]{1}=-1-1=-2 =-1- lim_{x to infty}sqrt[3]{1}=-1-1=-2](https://tex.z-dn.net/?f=%3D-1-+lim_%7Bx+to+infty%7Dsqrt%5B3%5D%7B1%7D%3D-1-1%3D-2)
Вычислили к чему стремиться степень. Теперь

Ответ: 4.
Поделим дробь и числитель и знаменатель на
Напишем для простоты только степень
Заметим, что слагаемое
Занесем
Заметим, что слагаемое
Вычислили к чему стремиться степень. Теперь
Ответ: 4.
Ответ дал:
0
Идеально. Большое спасибо!!!!
Похожие вопросы
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад