Предмет: Геометрия
Автор: kireevk003
Вопрос задан 2 года назад

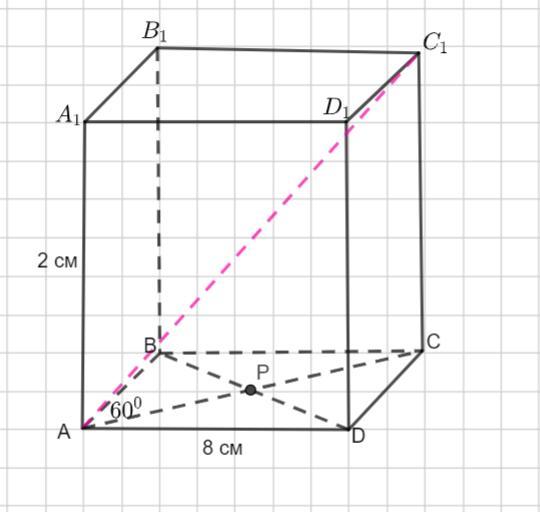
Основою прямої призми є ромб зі стороною 8 см і кутом 60 градусів . Висота призми дорівнює 2 см.
Знайдіть більшу діагональ призми.

Ответы

Ответ дал: lilyatomach

Ответ:

14 см.

Объяснение:

Рассмотрим прямую призму $ABCDA_{1} B_{1} C_{1} D_{1}$ . ABCD - ромб.

Так как ∠ А=60°, то Δ ABD- равносторонний( в равнобедренном треугольнике с углом 60° все углы будут по 60°) Тогда диагональ ромба BD равна тоже 8 см.

Найдем большую диагональ ромба АС . Так как диагонали ромба пересекаются под прямым углом и точкой пересечения делятся пополам, то ΔАВР - прямоугольный с гипотенузой АВ=8 см и катетом ВР=4см. Найдем другой катет по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

$AB ^{2} =AP^{2} +BP^{2} ;\\AP^{2} =AB ^{2} -BP^{2};\\AP= \sqrt{AB ^{2} -BP^{2}} ;\\AP= \sqrt{8^{2} -4^{2} } =\sqrt{(8-4)(8+4)} =\sqrt{4\cdot12} =\sqrt{4\cdot4\cdot3} =4\sqrt{3}$

Тогда диагональ АС в два раза больше

$AC= 2\cdot 4\sqrt{3} =8\sqrt{3}$ см.

Рассмотрим треугольник $ACC_{1}$ . Так как призма прямая, то этот треугольник прямоугольный.

Применим теорему Пифагора и найдем диагональ призмы $AC_{1}$

$AC_{1} ^{2} =AC^{2} +CC_{1} ^{2} ;\\AC_{1} = \sqrt{AC^{2} +CC_{1} ^{2} } ;\\AC_{1} = \sqrt{(8\sqrt{3} )^{2} +2^{2} } =\sqrt{64\cdot3+4} =\sqrt{192+4} =\sqrt{196} =14$