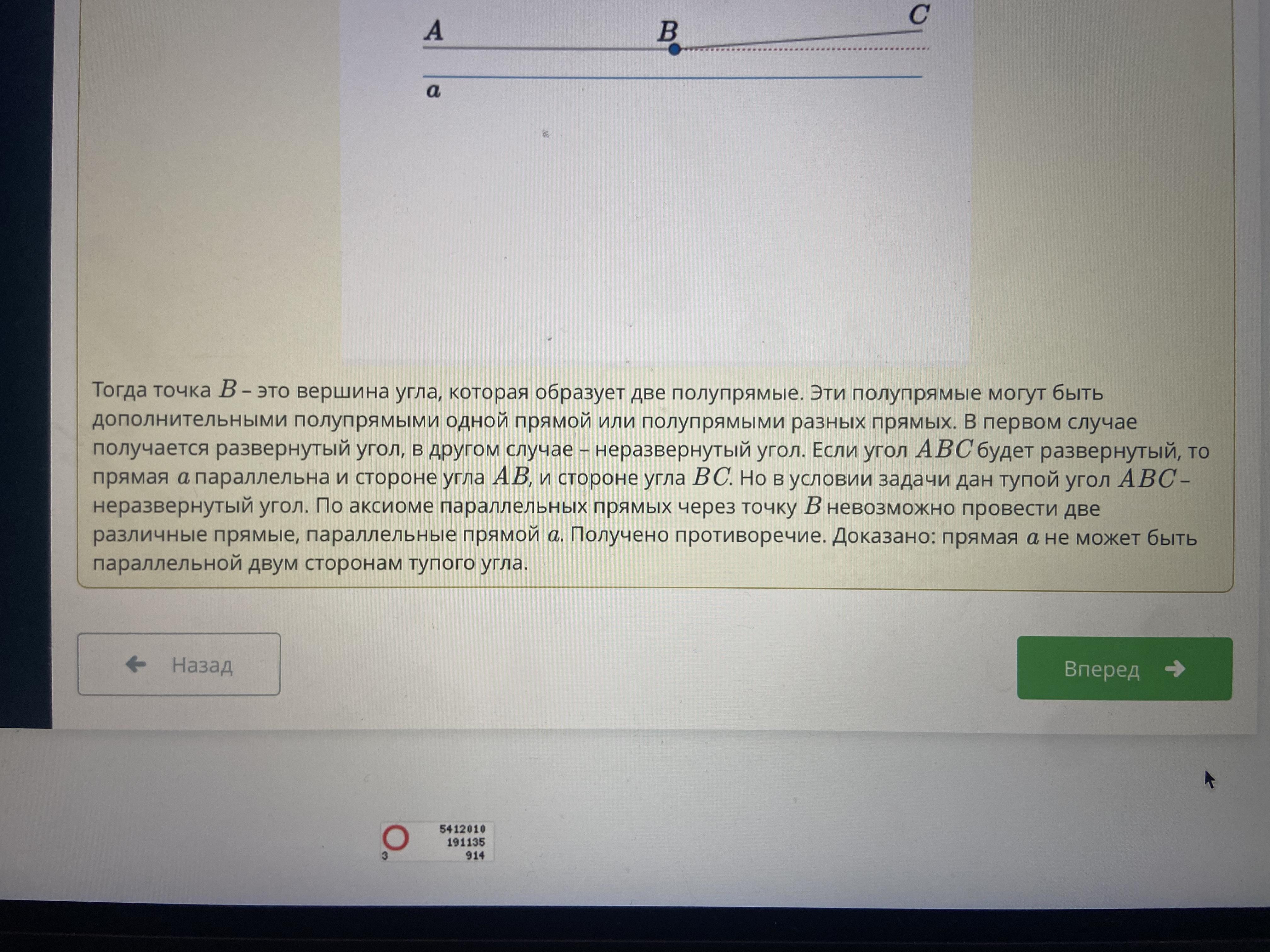
Дан тупой угол ABC. Докажи методом от противного, что прямая a, параллельная одной стороне угла, не параллельна другой его стороне.
Доказательство:
через точку, не лежащую на данной прямой,
Доказано: прямая a не может быть параллельной двум сторонам тупого угла.
Тогда точка B – общая точка прямой AB и прямой BC.
параллельную данной.
Значит, прямые AB и BC должны быть дополнительными полупрямыми.
По аксиоме параллельных прямых
Пусть a || AB и a || BC.
Получено противоречие: стороны тупого угла не могут быть дополнительными полупрямыми
можно провести на плоскости единственную прямую,

Помогите пожалуйста срочно надо