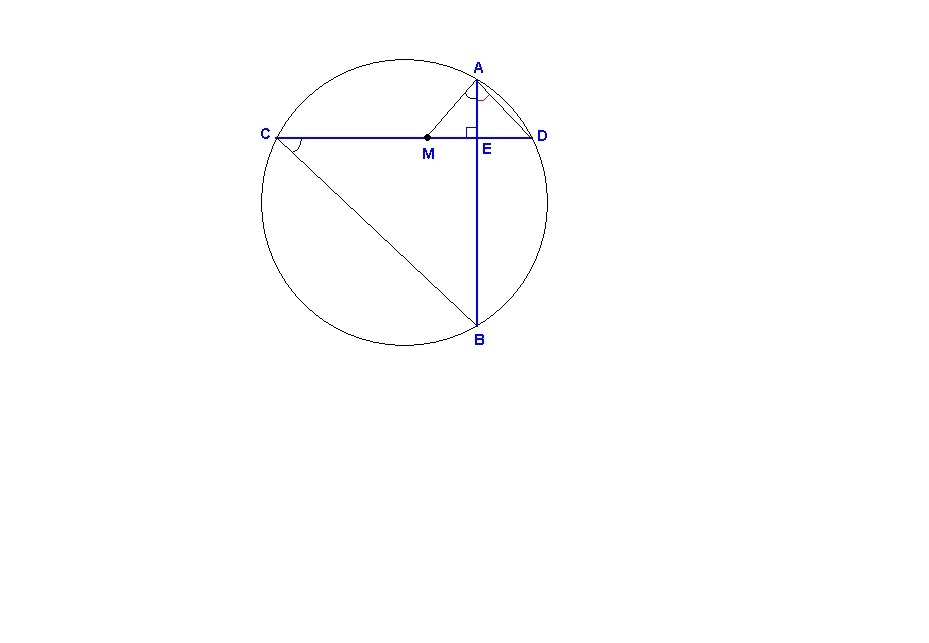
Хорды AB и CD некоторой окружности пересекаются в точке Е под прямым углом. CE=8, ED=2. M — такая точка на отрезке CD, что углы BCM и BAM равны. Найдите CM.
Ответы
Ответ дал:
0
∠BCD = ∠BAD как вписанные, опирающиеся на одну дугу BD,
∠BCD = ∠BAM по условию, ⇒
∠BAD = ∠BAM.
Тогда в треугольнике DAM АЕ - высота и биссектриса, значит треугольник равнобедренный, и АЕ является и медианой:
МЕ = ED = 2 см
СМ = СЕ - МЕ = 8 - 2 = 6 см
Приложения:
Похожие вопросы
2 года назад
2 года назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад
10 лет назад