Предмет: Алгебра
Автор: NotaHuman
Вопрос задан 2 года назад

30 Баллов. Дана функция y=f(x), где f(x)=12^x.
Вычислить: f(sin^2 x)⋅f(cos^2 x).
Пожалуйста, с объяснением.

Приложения:

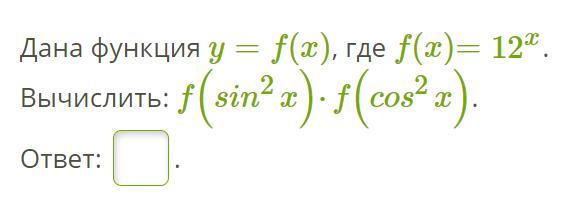
Ответы

Ответ дал: Universalka

$f(x)=12^{x} \\\\f(Sin^{2}x)=12^{Sin^{2}x}\\\\f(Cos^{2}x)=12^{Cos^{2}x} \\\\\\f(Sin^{2}x)*f(Cos^{2}x)=12^{Sin^{2}x}*12^{Cos^{2}x}=12^{Sin^{2}x+Cos^{2}x}=12^{1}=12\\\\Otvet:\boxed{12}$

При решении было применено основное тригонометрическое

тождество : Sin²α + Cos²α = 1

NotaHuman: Огромнейшее Вам спасибо!

Universalka: Пожалуйста

Аноним: Я проверила,всё правильно!

NotaHuman: Спасибо))

Похожие вопросы

Математика

1 год назад

957-(х+336)=438 468-(259-х)=382

Литература

1 год назад

как вы понимаете высказвание "от людей можно скрыться, а от себя куда уйдешь?"

Українська мова

2 года назад

Україна - це __, __, __. (треба продовжити речення)

Русский язык

2 года назад

Написать предложение в транскрипции "Каштанка бросилась вперёд, потом назад, ещё раз перебежала дорогу, но столяр точно сквозь землю провалился."

Математика

7 лет назад

как +, -, ×, : дроби?

Геометрия

7 лет назад

В треугольнике АВС известны стороны АВ = 30 см, ВС = 18 см и АС = 24 см. Сколько общих точек имеет окружность с центром в точке В и радиусом 18 см со стороной АС? Как можно более подробнее!

Химия

8 лет назад

Вот слова: атмосфера, вода, газ, растения, свет. Что объединяет все эти элементы? Какой процесс происходит в природе(из этих элементов)? Какое вещество образуется?

Биология

8 лет назад

1)что такое почка? 2)как различают почки 3)как почки могут распологаться на побегах? Установите взаимосвязь между нахождением почек на побеге и местомрасположением.4)какое строение имеет вегетативная

30 Баллов. Дана функция y=f(x), где f(x)=12^x. Вычислить: f(sin^2 x)⋅f(cos^2 x). Пожалуйста, с объяснением.

Ответы

30 Баллов. Дана функция y=f(x), где f(x)=12^x.
Вычислить: f(sin^2 x)⋅f(cos^2 x).
Пожалуйста, с объяснением.