ABCD ромб со стороной= а , угол А = 60 градусов. АМ перпендикулярна АВС. АМ= а2. Найти расстояние от точки М до прямой СД

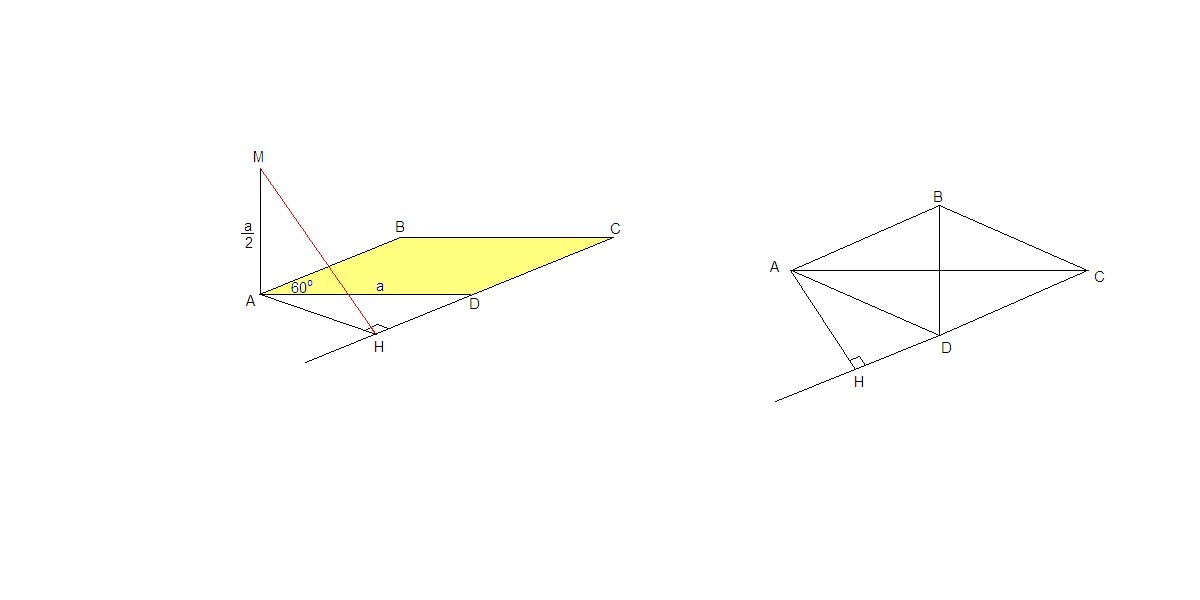
Проведем АН⊥CD, АН - проекция МН на плоскость АВС, значит и
МН⊥CD по теореме о трех перпендикулярах.
МН - искомое расстояние от точки М до прямой CD.

∠HDA = ∠BAD = 60° как внутренние накрест лежащие при пересечении параллельных прямых АВ и CD секущей AD.
ΔADH:  AH = AD · sin60° = a√3/2

ΔAMH:  по теореме Пифагора
               МН = √(МА² + АН² ) = √((a/2)² + (a√3/2)²) = √(a²/4 + 3a²/4) = √a² = a