Укажи, чему равна сумма S5, если bn = 4 ∙ 3n – 1. Помогите пожалуйста​

Сумма n членов геометрической прогрессии вычисляется по формуле:
Sn = (bn • q - b1) / (q - 1)

q = b(n+1) / bn - знаменатель геометрической прогрессии

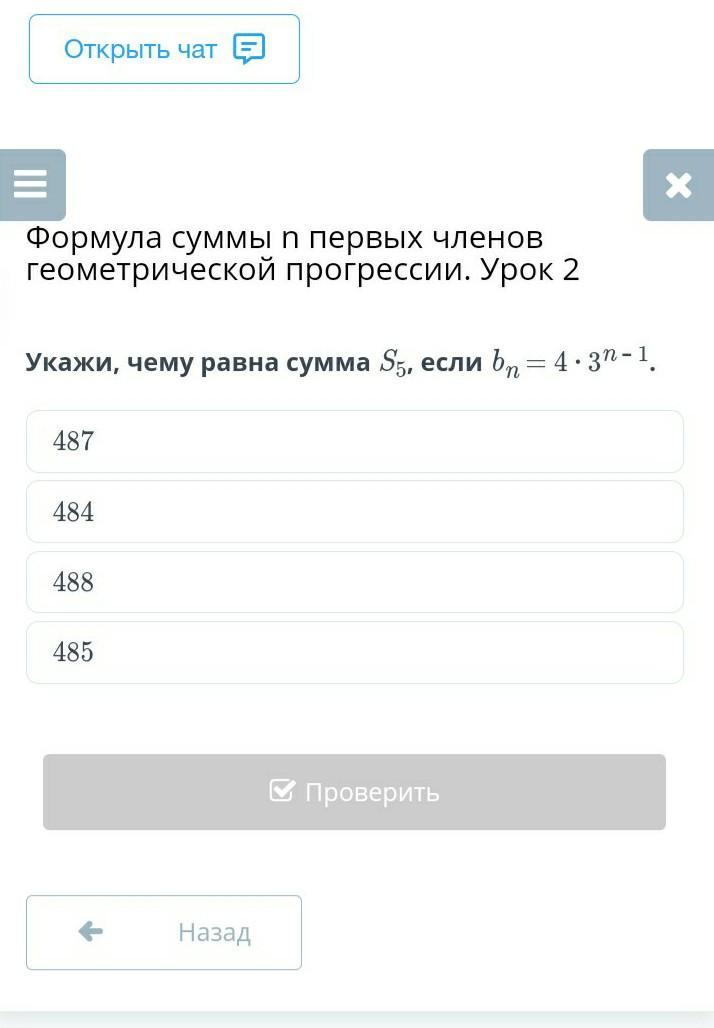
1) Если bn = 4 • 3^(n-1),
то:
b1 = 4 • 3^(1-1) = 4 • 3^0 = 4•1 = 4 - первый член
b2 = 4 • 3^(2-1) = 4 • 3^1 + 4 • 3 = 12 - второй член
b5 = 4 • 3^(5-1) = 4 • 3^4 = 4 • 81 = 324 - пятый член.

2) q = b(n+1) / bn
q = b2 / b1
q = 12 / 4 = 3

3) Sn = (bn • q - b1) / (q - 1)
S5 = (b5 • q - b1) / (q - 1)
S5 = (324 • 3 - 4) / (3 - 1) =
= (972 - 4) / 2 =
= 968 / 2 = 484 - сумма первых пяти членов заданной геометрической прогрессии.

Ответ: 484.


Ответ: