1)В окружность вписан правильный шестиугольник со стороной, равной 9. Найдите длину дуги окружности, стягиваемой стороной шестиугольника.

 

2) Найдите длину окружности, описанной около правильного треугольника, если радиус вписанной в этот треугольник окружности равен 7.

 

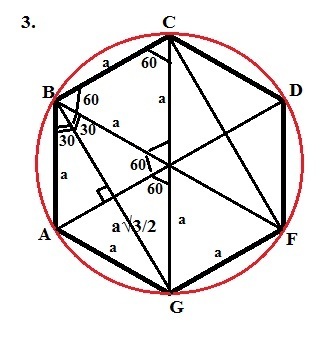
3) В правильном шестиугольнике ABCDFG проведены диагонали BC и CF. Докажите, что четырехугольник BCFG - прямоугольник, и выразите его стороны через сторону шестиугольника.

1) Радиус окружности, описанной около правильного шестиугольника, равен стороне этого шестиугольника. Тогда длина дуги окружности, стягиваемой стороной данного шестиугольника равна
L=2πR/6 = 2π9/6=3π.
Ответ: L=3π.
2) Центр вписанной и описанной окружности правильного треугольника лежит в одной точке - центре треугольника. Эта точка делит высоту правильного треугольника в отношении 2:1, считая от вершины.
причем 2/3 этой высоты - радиус описанной окружности, а 1/3 - радиус вписанной окружности.. Итак, R=2*7=14, а L=2πR или L=28π
Ответ: L=28π.
3) Диагонали правильного шестиугольника, пересекаясь в точке О, делят его на 6 равносторонних треугольника. Рассмотрим треугольник АОВ и ромб АВОG. <BOC=60°, а <GBO=30°. Следовательно, <GBC=90°.
Точно так же <BCF=90°. ВС=GF, как стороны правильного шестиугольника. CF=BG, как стороны равных треугольников ВОG и CDF.
Итак, ВСFG - прямоугольник, так как противоположные стороны попарно равны, а прилежащие к одной стороне углы равны 90°.
Что и требовалось доказать.
Если сторона шестиугольника равна "а", то ВС=FG=а, BG=CF= a√3 (по Пифагору из треугольника ВОG).