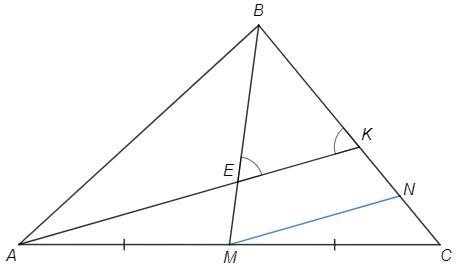
На медиане ВМ треугольника АВС взяли точку Е. Прямая АЕ пересекает сторону ВС в точке
К и образует равные углы с прямыми ВМ и ВС. Найдите ВС, если ВЕ=5, ЕМ=2.
Ответы
Ответ дал:
4
Проведем MN||AK
∠BMN=∠BEK, ∠BNM=∠BKE (соответственные)
∠BEK=∠BKE => ∠BMN=∠BNM => △MBN - равнобедренный, BN=BM=5+2=7
MEKN - равнобедренная трапеция (MN||EK, ∠BMN=∠BNM) => KN=EM=2
CM=MA, MN||AK => CN=KN=2 (т Фалеса)
BC =BN+CN =7+2 =9
Приложения:
Похожие вопросы
1 год назад
2 года назад
2 года назад
7 лет назад
7 лет назад