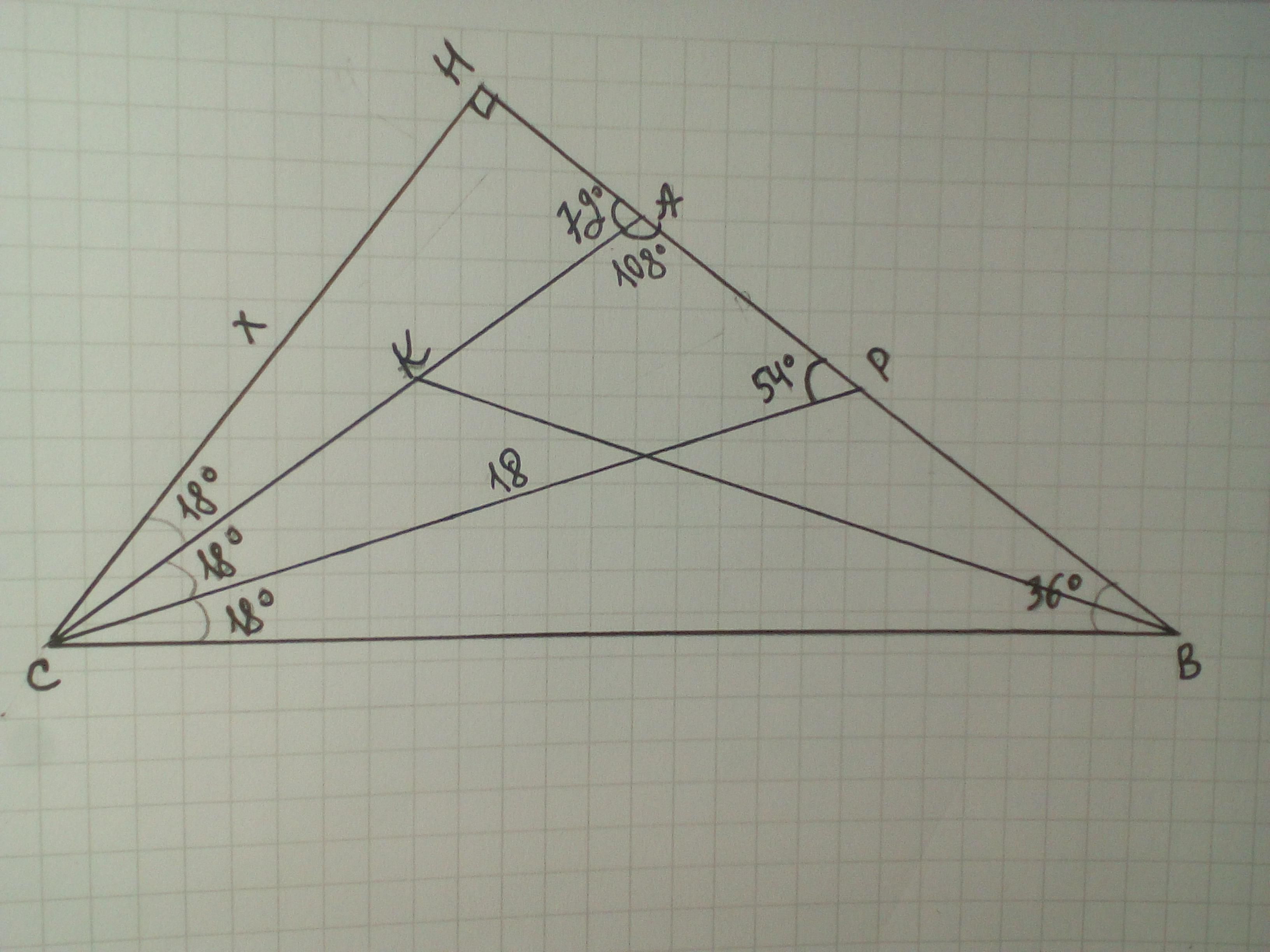
Дан равнобедренный треугольник ABC c AB = AC и угол B = 36°. Длина

биссектрисы, проведенной из вершины В, равна 18. Найдите длину высоты,

проведенной из вершины C.

СРОЧНО!!!

Ответ:

≈14,56 cм.

Объяснение:

Дано: ΔАВС - равнобедренный, АВ=АС,  ∠С=∠В=36°,  ВК и СР - биссектрисы, ВК=СР=18 см.  СН - высота. Найти СН.

Решение:

∠А=180-36-36=108°, ΔАВС - тупоугольный, значит, высота СН падает на продолжение стороны АВ.

Рассмотрим ΔСАН - прямоугольный, ∠САН=180-108=72°,  значит ∠АСН=90-72=18°.

Рассмотрим ΔРСН - прямоугольный,

∠РСН=18+18=36°,  тогда ∠СРН=90-36=54°

По теореме синусов

СН=СР*sin54°≈18*0,809≈14,56 cм.