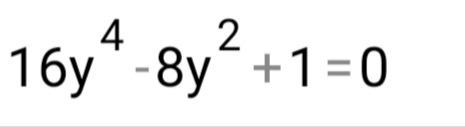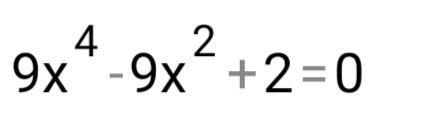Решите биквадратное уравнение!!!
||||Пожалуйста!|||
Всего лишь две!

Приложения:

Ответы

Ответ дал: EADF

Пошаговое объяснение:

16y⁴-8y²+1=0

y²=x (замена)

16x²-8x+1=0

D=b²-4ac=(-8)²-4×16×1=64-64=0 (1 корень)

$\displaystyle x = - \frac{b}{2a} = \frac{8}{2 \times 16} = \frac{8}{32} = \frac{1}{4}$

Обратная замена: x=y²

$\displaystyle y = \sqrt{x}$

$\displaystyle y = \sqrt{ \frac{1}{4} } = \frac{1}{2}$

Ответ: у=0,5

________________________________

9х⁴-9х²+2=0

Заменяем: x²=t

9t²-9t+2=0

D=b²-4ac=(-9)²-4×9×2=81-72=9 (два корня)

$\displaystyle t_{1, 2} = \frac{-b \pm \sqrt{D}}{2a} = \frac{9 \pm \sqrt{9}}{2 \times 9} = \frac{9 \pm 3}{18} = \frac{3(3 \pm 1)}{18}=\frac{3 \pm 1}{6}$

$\displaystyle t_{1} = \frac{3+1}{6} = \frac{4}{6} = \frac{2}{3}$

$\displaystyle t_{2} = \frac{3-1}{6} = \frac{2}{6} = \frac{1}{3}$

Обратная замена: t=x²

$\displaystyle x = \sqrt{t}$

Ответ:

$\displaystyle x_{1} = \sqrt{ \frac{2}{3} }$

$\displaystyle x_{2} = - \sqrt{ \frac{2}{3}}$

$\displaystyle x_{3} = \sqrt{ \frac{1}{3} }$

$\displaystyle x_{4} = -\sqrt{ \frac{1}{3} }$

EADF: Если вам понравился ответ, то поставьте лайк, 5звезд (если ответ помог) и отметьте как лучший. Я старался подробно расписать решение и объяснить.

Аноним: Реально спасибо, спасибо что запарился

EADF: (◠‿◕) правда запарился. Рад помочь

Похожие вопросы

Алгебра

1 год назад

Решите уравнение. Одна вторая х(3 степень) - 1 =31

Химия

1 год назад

ПОМОГИТЕ ПОЖАЛУЙСТА С чем реагирует калий гидроксид Написать реакции (минимум 3)

Другие предметы

2 года назад

что такое кибернетика