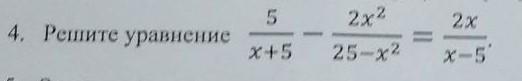Предмет: Алгебра
Автор: Аноним
Вопрос задан 2 года назад

< >

Помогите с алгеброй

Приложения:

Ответы

Ответ дал: MatemaT123

Ответ:

Корней нет.

Объяснение:

$\frac{5}{x+5}-\frac{2x^{2}}{25-x^{2}}=\frac{2x}{x-5};$

$\frac{5}{x+5}+\frac{2x^{2}}{x^{2}-25}=\frac{2x}{x-5};$

$\frac{5}{x+5}+\frac{2x^{2}}{(x-5)(x+5)}=\frac{2x}{x-5};$

ОДЗ:

$x+5 \neq 0 \Rightarrow x \neq -5;$

$x-5 \neq 0 \Rightarrow x \neq 5;$

Решение:

$\frac{5}{x+5}+\frac{2x^{2}}{(x-5)(x+5)}=\frac{2x}{x-5};$

$\frac{5(x-5)}{(x-5)(x+5)}+\frac{2x^{2}}{(x-5)(x+5)}=\frac{2x(x+5)}{(x-5)(x+5)};$

$5(x-5)+2x^{2}=2x(x+5);$

$5x-25+2x^{2}=2x^{2}+10x;$

$5x-10x+2x^{2}-2x^{2}=25;$

$-5x=25;$

$x=-5;$

Единственный корень не удовлетворяет ОДЗ ⇒ корней нет.

Похожие вопросы

Українська література

1 год назад

хто є оповідачем у пісні «віють вітри, віють буйні»? поміркуйте чому в цій пісні для передавання почуттів використано саме монолог

Русский язык

1 год назад

ДЛЯ ЧЕГО НУЖЕН КОЛБА

Английский язык

2 года назад

помогите ребята: Catherine is not at home. ... at work. "... your coat" "Oh , thank you very much" ребята help ME помогите до завтра надо. 20 баллов даю!!!

Українська література

2 года назад

Вiрш про рiдну мову 6-8 рядкiв!!!

Математика

7 лет назад

Имеется два сплава. Первый сплав содержит 5% меди, второй — 14% меди. Масса второго сплава больше массы первого на 5 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу

Литература

7 лет назад

Кто посоветовал мальчику попросить у бабушки прощения? А) Тётя Феня Б) Дедушка В) тётка Васеня

Литература

9 лет назад

Какие есть рассказы о любознательности? напишите 3-4,пожалуйста Т.е название рассказа и автора НО ЧТОБЫ ОБЯЗАТЕЛЬНО ЗАТРАГИВАЛ ТЕМУ ЛЮБОЗНАТЕЛЬНОСТИ ПОДСКАЖИТЕ ПОЖАААЛУЙСТА!!

Литература

9 лет назад

Не ужинать — святой закон, Кому всего дороже легкий сон. объясните смысл этих строк.

Помогите с алгеброй​

Ответы

Помогите с алгеброй