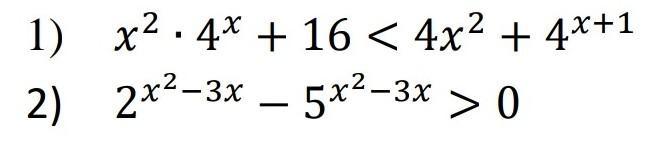Решите неравенство.​

Объяснение:

1)

x²·4ˣ - 4·4ˣ - (4x² - 16) < 0

4ˣ · (x² - 4) - 4 · (x² - 4) < 0

(4ˣ - 4)(x² - 4) < 0

Заметим, что принимает значения тех же знаков, что и

x - 1, а значит наше неравенство равносильно более простому:

(x - 1)(x - 2)(x + 2) < 0, которое решается методом интервалов:

x = -2; x = 1; x = 2 - обращает в 0 соответствующие скобки

Рисуем схему (см. рисунок)

Получаем: x∈(-∞; -2)∪(1; 2)

2)

Так как - показательная функция возрастает, получаем:

x² - 3x < 0

x·(x - 3) < 0

0 < x < 3

x ∈ (0; 3)