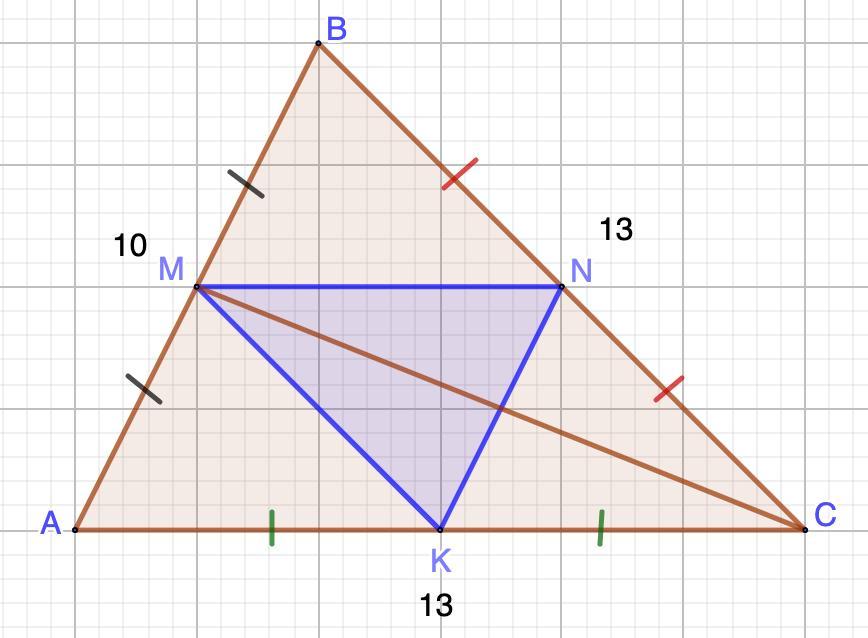
еугольники abc точки м н к середины сторон аб бц ац найдите площадь треугольника мнк если аб равно 10 бц равно 13 ац равно 13 дайте просто ответ пж даю 20 баллов

Ответ:

15 ед².

Объяснение:

Дано: ΔАВС.

AM = MB; BN = NC; AK = KC

AB = 10; AC = 13; BC = 13.

Найти: S (ΔMNK)

Решение:

Так как точки M, N, K - середины сторон AB, BC, AC соответственно,

то MN, NK, MK - средние линии ΔАВС.

1. Рассмотрим ΔАВС.

ВС = АС = 13 ⇒ ΔАВС - равнобедренный.

Проведем СМ - медиану.

АМ = МВ = 10 : 2 = 5.

• В равнобедренном треугольнике высота является медианой и биссектрисой.

⇒ СМ - высота.

2. Рассмотрим ΔАМС - прямоугольный.

По теореме Пифагора:

3. Найдем площадь ΔАВС:

• Средняя линия отсекает треугольник, подобный исходному и его площадь равна одной четвёртой площади исходного треугольника.

⇒

Найдем площадь ΔMNK: