4. В треугольнике ВМС стороны ВМ и МС равны, точка А лежит на биссектрисе МК, Докажите, что АВ= АС.

Ответ:

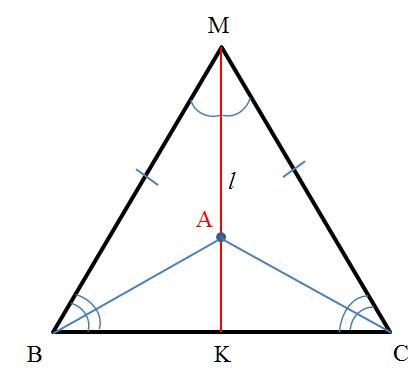
Дано (см. рисунок 1):

 ΔBMC

 BM=MC

 ∠BMK=∠CMK

 A∈MK  

Доказать: АВ = АС.

Доказательство.

Так как  BM=MC, то треугольник BMC равнобедренный. Вспомним свойство равнобедренных треугольников:

В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

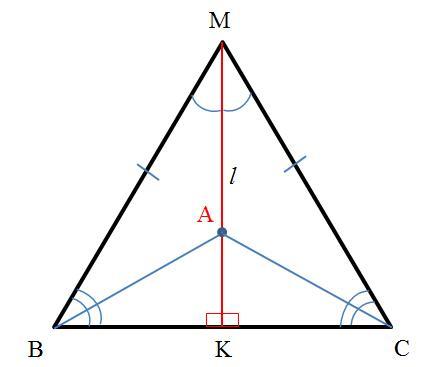
Тогда, во-первых, биссектриса MK является медианой, откуда следует BK=KC, во-вторых, биссектриса MK является высотой, откуда следует, что треугольники AKB и AKC прямоугольные (см. рисунок 2).

В прямоугольных треугольниках AKB и AKC катет AK общий, а катеты BK и KC равны. Тогда, по признаку равенства прямоугольных треугольников по двум катетам треугольники AKB и AKC равны, отсюда АВ = АС.