Предмет: Математика
Автор: ponhara26
Вопрос задан 10 лет назад

помогите пожалуйста, как найти область определения функции y=3x-2x^2 (под корнем)?

Ответы

Ответ дал: Аноним

Задание. Найти область определения функции y = √(3x-2x^2).
Решение:
Подкоренное выражение должен принимать неотрицательные значения, т.е. $3x-2x^2 geq 0$ . Для удобства умножим обе части неравенства на (-1), при этом знак неравенство меняется на противоположный, т.е. $2x^2-3x leq 0.$
Неравенство будем решать методом интервалов.
Приравниваем к нулю. $2x^2-3x=0;,,,,,,x(2x-3)=0$ . Произведение равно нулю, если хотя бы один из множителей обращается в нуль, т.е. $x_1=0$ и $2x-3=0$ откуда $x=1,5.$

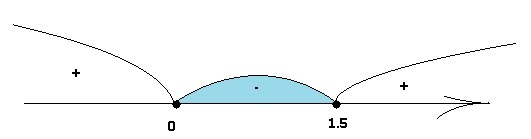
Знаки на интервалах.
Определим знак справа, для этого возьмём любое значение х>1.5, т.е., например, возьмём х=2. Подставив в левой части неравенства, получим $2cdot2^2-3cdot2=8-6=2 textgreater 0$ , следовательно, справа будет знак "+" дальше знаки чередуются с "-" и "+". Искомый промежуток $x in [0;1.5].$

Область определения функции: $D(f)=[0;1.5].$

Ответ: $D(f)=[0;1.5].$

Приложения: