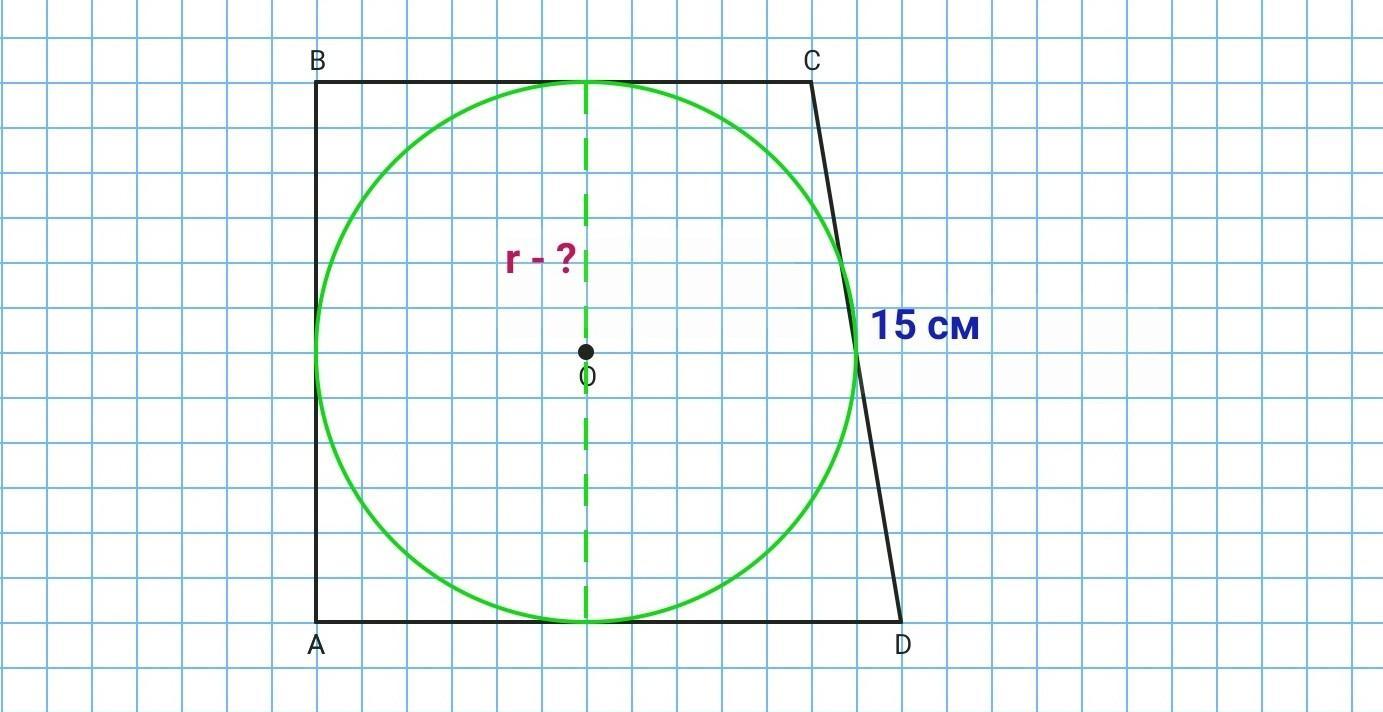
У прямокутну трапецію, більша бічна сторона якої дорівнює 15 см, вписано коло. Знайдіть радіус кола, якщо периметр трапеції дорівнюють 50 см.

Ответ:

5 см

Объяснение:

• Якщо сума основ трапеції дорівнює сумі її бічних сторін, то в таку трапецію можна вписати коло, і навпаки.

AB+CD=BC+AD

Так як периметр трапеции доривнюе 50 см , маємо:

AB+CD=50:2=25 см

За умовою СD=15 =>

AB+15=25

AB=10

Бічна сторона AB є перпендикулярною до основ і дорівнює висоті трапеції. Висота трапеції дорівнює 2×r. r - радіус вписаного кола.

2×r=10,

r = 10÷2=5 см