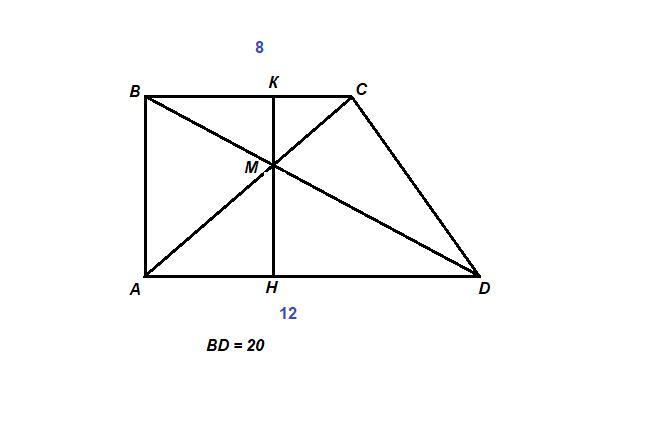
В прямоугольной трапеции ABCD (угол BAD=90 градусов) основаниями AD=12 и BC=8 большая диагональ BD=20. Диагонали AC и BD пересекаются в точке M.
а) докажите, что треугольники BMC и DMA подобны.
б) найдите площадь треугольника BMC

Ответ:

б)

Объяснение:

а)

∠BMC = ∠DMA как вертикальные,

∠СВМ = ∠ADM как накрест лежащие при пересечении параллельных прямых AD и ВС секущей BD, значит

ΔBMC ~ ΔDMA по двум углам.

б)

Из прямоугольного треугольника ABD по теореме Пифагора:

АВ = √(BD² - AD²) = √(20² - 12²) = √(400 - 144) = √256 = 16

Проведем высоту КН через точку пересечения диагоналей.

КН = АВ = 16

Отношение высот подобных треугольников, проведенных к сходственным сторонам, равно коэффициенту подобия.

ΔBMC ~ ΔDMA, значит

Пусть МК = х, тогда МН = КН - х = 16 - х

3x = 2(16 - x)

3x = 32 - 2x

5x = 32

x = 6,4

Площадь треугольника ВМС: