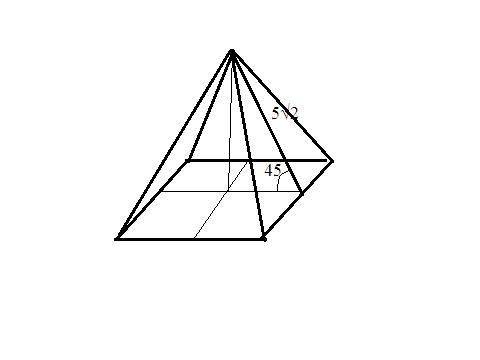
В правильной четырехугольном пирамиде апофема равна ,а боковая грань образует с плоскостью основания угол 45° . Найти объем пирамиды.
С рисунком, если можно.

Ответ:

Объяснение:

Апофема - высота боковой грани пирамиды образует с высотой пирамиды и половиной основания прямоугольный равнобедренный треугольник с гипотенузой - 5√2 (апофема) и равными катетами (высота и половина длины стороны основания). По т. Пифагора h=5 ед, сторона квадрата основания - 10 ед;

V=S*h/3=10²*5/3=500/3 ед³.