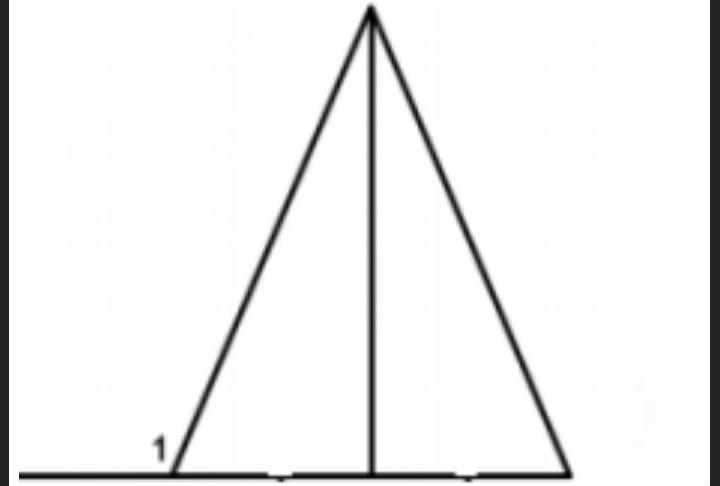
В равнобедренном треугольнике КСМ основанием КМ проведена медиана СА. Найдите градусные меры углов САМ и СМК, если внешний угол NКС равен 109°.​

СК=КМ - т.к. треугольник СКМ равнобедренный

СА - медиана, а в р/б треугольнике является также высотой и биссектрисой

Следовательно, угол САМ - прямой, т.е равен 90

Угол NKC и угол СKA - смежные углы, значит их сумма равна 180, т.е NKC+CKA= 180

CKA= 180- NKC

CKA=180-109=71

Углы СКА , СМК - углы при основании равнобедренного треугольника, значит они равны: CKM=CMK=71

Ответ: САМ= 90, СМК = 71