Найдите высоты треугольника со сторонами 5, 6 и 7.

Ответы

Ответ дал: ReMiDa

Ответ:

$BH=\dfrac{12\sqrt{6} }{7} \\\\AK=2\sqrt{6} \\\\CM=\dfrac{12\sqrt{6} }{5}$

Объяснение:

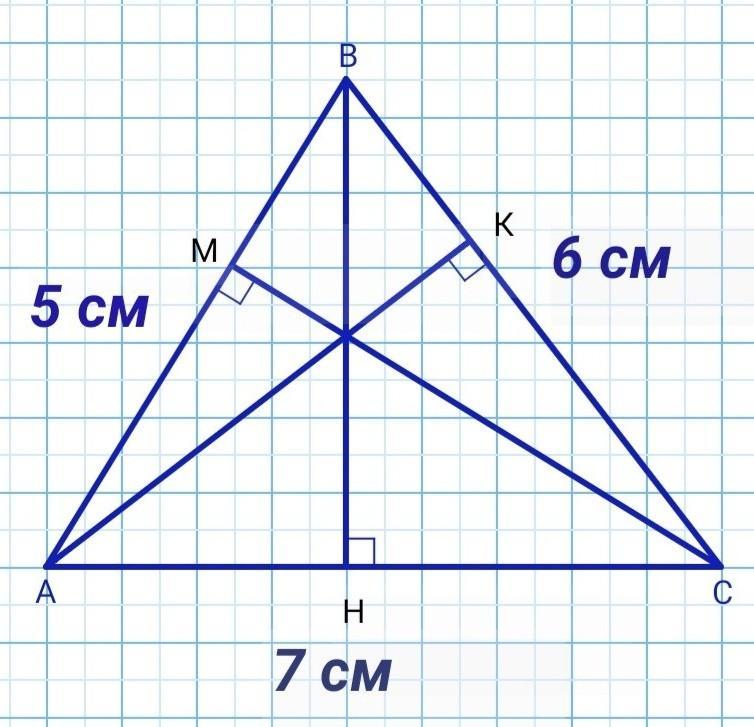
Дано: ΔАВС, АВ=5 см, ВС= 6 см, АС= 7 см, ВН⊥АС, СМ⊥АВ, АК⊥ВС

Найти: ВН, СМ, АК

Найдём площадь ΔАВС по формуле Герона:

$S= \sqrt{p(p-a)(p-b)(p-c)$

где a, b, c - стороны треугольника, р - полупериметр.

$p=\dfrac{a+b+c}{2} =\dfrac{5+6+7}{2} = 9$ см

$S = \sqrt{9(9-5)(9-6)(9-7)} =\sqrt{9*4*3*2} =3*2*\sqrt{3*2} =6\sqrt{6}$ cм²

С другой стороны, площадь треугольника равна произведению половины основания треугольника (a) на его высоту (h), проведенную к этому основанию:

$S = \dfrac{1}{2} * a*h$

Таким образом находим высоты:

1) ВН

$S = \dfrac{1}{2} * AC*BH\\\dfrac{1}{2} *7*BH=6\sqrt{6} \\BH=\dfrac{6\sqrt{6}*2 }{7} =\dfrac{12\sqrt{6} }{7}$

2) AK

$S=\dfrac{1}{2} *BC*AK\\\dfrac{1}{2} *6*AK=6\sqrt{6} \\AK=\dfrac{6\sqrt{6}*2 }{6} =2\sqrt{6}$

3) CM

$S = \dfrac{1}{2} *AB*CM\\ \dfrac{1}{2} *5*CM = 6\sqrt{6} \\CM=\dfrac{6\sqrt{6}*2 }{5} =\dfrac{12\sqrt{6} }{5}$

Приложения:

Похожие вопросы

Математика

1 год назад

Физика

1 год назад

Русский язык

2 года назад

Математика

2 года назад

Алгебра

7 лет назад

Химия

7 лет назад

Музыка

9 лет назад

Литература

9 лет назад