Допоможіть
Буду щиро вдячна

Приложения:

Ответы

Ответ дал: vladyatsuk

Ответ:

див. фото

Объяснение:

Приложения:

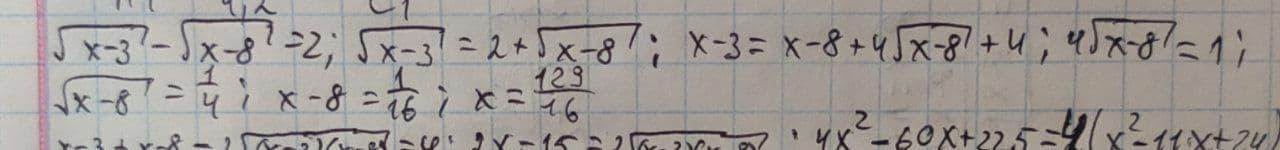
vladyatsuk: Прошу ще відмітити як найкращу відповідь і поставити 5 зірок )

Ответ дал: sangers1959

Объяснение:

$\sqrt{x-3}-\sqrt{x-8}=2\\\sqrt{x-3}=2+\sqrt{x-8} .$

ОДЗ: х-3≥0 х≥3 х-8≥0 х≥8 ⇒ х∈[8;+∞).

$(\sqrt{x-3})^2=(2+\sqrt{x-8})^2\\x-3=2^2+2*2*\sqrt{x-8} +(\sqrt{x-8})^2\\x-3=4+4*\sqrt{x-8}+x-8\\4*\sqrt{x-8}=1\ |:4\\\sqrt{x-8} =\frac{1}{4}\\(\sqrt{x-8})^2 =(\frac{1}{4})^2\\x-8=\frac{1}{16}\\x=8\frac{1}{16}.$

Ответ: x=8¹/₁₆.

Похожие вопросы

Русский язык

1 год назад

Помогите пожалуйста, объясните что такое причасные и деепричасные обороты с примерами и развернуто

Русский язык

1 год назад

Друзья мои, внушайте людям веру и чаще говорите : „Добрый день!”И следуйте хорошему примеру Продляйте добрым словом Жизнь людей! Определить тему отрывка ключевые слова раскрывающие тему

Алгебра

2 года назад

Два фильтра марки «Родник» очищают 1000 л воды за 5 часов. За сколько часов один такой фильтр очистит 600 л воды? Решение: Ответ: Обьязательно!!!! Помоги, от этого решится исход моей четверти

Русский язык

2 года назад

Выписать из предложения предлоги: И все это благодаря тому,что у него есть память.

География

7 лет назад

Сделайте пожалуйста информацию о паровых машинах

Математика

7 лет назад

28(1-4х)=7 решите плиз

Информатика

9 лет назад

Восемь школьников оставались в классе на перемене, и один из них разбил окно. На вопрос директора, кто это сделал, были получены следующие ответы: Егор: «Разбил Андрей»! Света: «Вика разбила»!

Алгебра

9 лет назад

$left { {{y+4 leq 0} atop {5y+15 leq 0}} right.$ Пожалуйста!!!

Допоможіть Буду щиро вдячна

Ответы

Допоможіть
Буду щиро вдячна