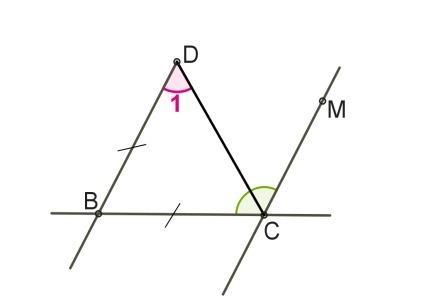
Известно, что в данной ситуации: DB=BC; DB∥MC; ∡BCM = 156°. Рассчитай величину ∡1.

∡1 =

Ответ:

78°

Пошаговое объяснение:

По условию  DB∥MC, отсюда следует, что  ∠1 = ∠DCM как накрест лежащие при параллельных прямых DB∥MC  и секущей DC.

По второму условию DB=BC, значит ΔCBD равнобедренный, и тогда

∠1 = ∠DCВ, как углы при основании равнобедренного треугольника.

Объединим эти два вывода и получим, что   ∠DCM = ∠DCВ.

Тогда каждый из этих углов равен 156° : 2 = 78°.

И, следовательно  ∠1 = 78°

ответ

∠1 = 78°